Grafická data

Grafická data se obvykle dělí na data vektorová a bitmapová (rastrová)

Vektorová data: vektor je v souvislosti s grafickými soubory chápán v „tradičním“ slova smyslu, tj. je ztotožňován s s „orientovanou“ úsečkou, tj. úsečkou, na které rozlišujeme počáteční a koncový bod, popř. s veličinou která je určena velikostí, směrem a orientací. Jak vyplývá z předcházejícího textu, v matematice je pojem vektoru podstatně širší. Pojem vektoru v počítačové grafice vychází spíše z matematického pojetí. V zásadě lze říci, že vektorový grafický soubor obsahuje informace o objektech složených z křivek a jednoduchých těles, které umožňují jejich geometrickou konstrukci. Je-li takto uložena např. kružnice, soubor neobsahuje informace o všech jednotlivých bodech, které na ní leží. Informuje o tom, že se jedná o kružnici, dále obsahuje souřadnice jejího středu, jednoho bodu, který na ní leží a poslední bod určuje rovinu její konstrukce. Připojeny jsou rovněž informace o barvě objektu a tloušťce čáry, kterou má být sestrojen. Program, pro který jsou tato data určena, musí být schopen tyto informace správně přečíst a musí obsahovat algoritmus, který na základě těchto informací kružnici sestrojí. Vektorová data jsou typická např. pro technické výkresy.

Bitmapová (rastrová) data: neobsahují „vektorové“ informace o uloženém objektu. Z těchto dat nelze (alespoň ne jednoduše) zjistit, zda se obraz skládá z obdélníků, kružnic, či jehlanů. Soubor obsahuje informace o velikosti obrazu, o způsobu případné komprese a kódování barev. Samotný obraz je uložen jako matice, jejíž každý prvek znamená jeden bod obrazu. Rastrově jsou ukládány buď informace, které již nebudou

dále upravovány systémem, kterým byly vytvořeny (např. žánrový pohled na strojní součást), nebo obrazy, které nebyly pořízeny počítačem (např. fotografie). Na rastrovém principu funguje většina zobrazovacích zařízení (monitory, jehličkové, inkoustové i laserové tiskárny, televize apod.).

Rastrová data ukládáme data jako souřadnice bodů, které jsou v souladu s tradiční euklidovskou geometrií modelovány jako bezrozměrné objekty. Zobrazovací plocha výstupního zařízení (ať již monitoru či tiskárny, koneckonců i sítnice lidského oka) je však fyzické zařízení a „body bez rozměrů“ zobrazovat resp. vnímat neumí. Místo pojmu „bod“ je proto používán pojem „pixel“ (novotvar z anglického „picture element“) jako „nejmenší zobrazitelný útvar“. Při matematickém modelování je třeba rozlišovat pixely ve smyslu „logickém“ (tj. výstupní zařízení chápat jako množinu izolovaných euklidovských bodů) a ve smyslu „fyzickém“ (tj. výstupní zařízení jako „množina elementárních plošek“). Současná počítačová literatura tyto pojmy většinou vůbec nerozlišuje a v tom případě chápe pixel spíše ve smyslu „fyzickém“. Nicméně i v případě, že tyto pojmy rozlišovány jsou, je jejich vymezení velmi vágní a často zcela chybné, a to i v renomované zahraniční literatuře. Můžeme se např. dočíst, že „Fyzické pixely jsou body, které jsou používány pro zobrazování na výstupním zařízení… Tyto pixely jsou přímo ovládány hardwarem výstupního zařízení… V praxi zobrazovací zařízení překrývá nebo skládá vedle sebe více barevných bodů tak, aby se vytvořil jediný pixel.“ Bez dalšího vysvětlení je pak výstupní zařízení ilustrováno jako šachovnice, tj. množina různobarevných čtverců, které jsou (chápány jako otevřené množiny) po dvou disjunktní. Ve smyslu této ilustrace jsou pak dále používány. Takto chápané „fyzické pixely“ však nejsou na výstupním zařízení vůbec závislé a nemohou jím být ani ovládány. Nejedná se totiž o fyzické pixely samotné, ale o jejich matematické modely. Vzhled „fyzických pixelů přímo ovládaných hardwarem“ je závislý na konkrétním výstupním zařízení.

Fyzické pixely přímo ovládané hardwarem vidíme na následujícím obrázku. Vlevo je mikrosnímek obrazovky monitoru Samsung. Levá část snímku je „bílá plocha“, na pravé se pravidelně střídají „černé a bílé body“. Vpravo je pak mikrosnímek části výstupu z tiskárny Canon BJC250.

Matematický model fyzických pixelů: mikrosnímky již zmíněného monitoru (levá část obrazu) a matematického modelu téže situace. Takto modelované „fyzické pixely“ používají dnes prakticky všechny grafické aplikace.

Vzhledem k tomu, že pojem fyzický pixel je již poměrně běžně používán, přidržíme se tohoto označení ve speciálních případech i my. Navzdory poněkud nevhodnému termínu se však nebude jednat o pixely implementované na konkrétních zařízeních, ale o matematický model pixelů, který abstrahuje od vlastností daných konkrétním zařízením a ponechává jedinou, která je těmto zařízením společná – totiž nenulové rozměry. Vzhledem k tomu, že výstupní zařízení počítačů jsou téměř výhradně obdélníková, budeme definovat digitální rovinu i fyzické pixely jako obdélníky. Pixely budeme modelovat jako po dvou disjunktní, přestože ani tato vlastnost není na konkrétních zařízeních (zvláště při nastavení příliš vysokého rozlišení) splněna. Kvalitní výstupy však vyžadují, aby se „fyzické pixely ovládané hardwarem“ překrývaly co možná nejméně. Existují praktická omezení vzdálenosti zobrazovaných pixelů. Budeme-li po zobrazovací ploše požadovat příliš velkou rozlišovací schopnost, může se stát, že sousední fyzické pixely se budou překrývat, či jinak spolu kolidovat a výsledkem bude zhoršení kvality obrazu.

Velikost obrázku jsme většinou zvyklí udávat v délkových jednotkách (např. v centimetrech). Nedocenění významu velikosti fyzických pixelů může vést k zásadním omylům, a to i u profesionálních grafiků. Rastrová data jsou interpretována jako matice, jejichž každý prvek znamená jeden pixel obrazu. O kvalitě výsledného výstupu tak mimo jiné rozhoduje velikost pixelů nebo častěji udávané rozlišení, tj. „počet bodů na palec“

Rozlišení 800´600 může poskytovat vysoce kvalitní (malý) obraz na čtrnáctipalcovém monitoru a díky omezené rozlišovací schopnosti lidského oka zde již nemá smysl použít rozlišení větší. Totéž rozlišení však bude asi nedostatečné na monitoru jednadvacetipalcovém. Obraz s rozlišením 2000´3000 bude kvalitně vytištěn na listu A4, na listu A3 bude kvalita téhož obrazu podstatně horší. Z tohoto důvodu se v technické praxi udávají rozlišení tiskáren v přepočtu na jednotku délky, jednotkou je DPI - Dots Per Inch (počet bodů na palec).

Vektorový grafický soubor obsahuje informace o objektech složených z křivek, ploch či jednoduchých těles, které umožňují jejich geometrickou konstrukci. „Fyzická velikost“ takto reprodukovaného objektu (tj. velikost udávaná v délkových jednotkách) může být optimalizována dle konkrétního výstupního zařízení. Tuto situaci ilustruje připojený obrázek.

Je-li do rastrových dat s nízkým rozlišením (např. do obrázku) dodáno písmo a vše opět uloženo jako obrázek, pak písmo nemůže mít větší rozlišení, než původní obrázek. Je-li však obrázek uložen jako rastr a písmo ve vektorové podobě, může být text dle možností výstupního zařízení vytištěn podstatně kvalitněji, než obrázek, do kterého je vložen. Odtud pramení názor, že pro tiskařské účely jsou vektorová data vhodnější. Většinou slýcháme, že pro tiskařské účely je třeba text dodávat vždy vektorově, neboť rastrová písmena jsou „zubatá“, „chlupatá“ apod. Tento názor zastává řada tiskařů, počítačových grafiků a průmyslových designérů. Nepřímo je tak prezentován zcela chybný názor, že lidské oko má nekonečnou rozlišovací schopnost a také tiskařský proces vyprodukuje zcela dokonalý výstup. Vektorová data mají nekonečné rozlišení, stejně nekonečné je zřejmě i rozlišení tiskárny a osvitového zařízení, čtyři fólie budou na sebe položeny s přesností nejméně na průměr atomového jádra, fólie stejně jako papír jsou zcela homogenní a nemají žádnou strukturu. Za těchto podmínek je takový názor správný. Žádná z těchto podmínek však ani zdaleka nemůže být splněna.

Na těchto obrázcích můžeme porovnat výsledky reálného tiskařského procesu. Bílé písmeno je rastrové, bylo uloženo spolu s obrazem s rozlišením 600 DPI. Písmeno vpravo je do obrázku z tímtéž rozlišením dodáno vektorově. Při této kvalitě vstupních dat nejsme schopni zaznamenat rozdíl v písmu, (natož „zubatost“ či „chlupatost“) ani na mikrofotografii, kde je již zcela zřetelná struktura křídového(!) papíru. (mikrofotografie výtisku je pořízena s rozlišením 3600 DPI).

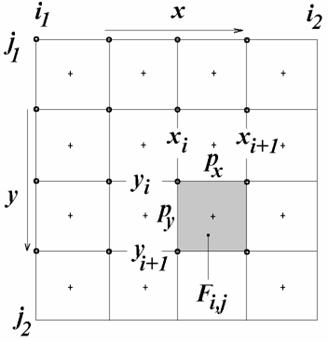
Logické pixely: Jestliže chceme na fyzický pixel odkazovat souřadnicemi, pak v řadě grafických aplikací je důležité také to, na který euklidovský bod fyzického pixelu odkazujeme - zda na střed, některý z vrcholů (a na který) – viz obrázek, či na nějaký jiný bod. Body, na které odkazujeme souřadnicemi, se v literatuře obvykle nazývají logické pixely a  jejich případně potřebná výše uvedená specifikace se nazývá adresace či mapování. Vzhledem k tomu, že pojem adresace je používán také ve smyslu adresy bodu v operační paměti počítače, pro určení polohy logického pixelu budeme používat termín mapování.

Logické pixely jsou matematické body. Specifikují polohu, ale fyzicky nezabírají žádnou plochu. Mapování (tj. vzájemné přiřazení) mezi fyzickými a  logickými pixely musí odpovídat skutečné velikosti a uspořádání fyzických pixelů. Na jednotlivé logické pixely se odkazujeme tzv. světovými souřadnicemi. Ve většině aplikací jsou to čísla typu integer (celá čísla) popř. word (nezáporná celá čísla), kde levý horní roh zobrazovacího zařízení má souřadnice [0;0], souřadnice sousedních pixelů se liší o jedničku. Tato souřadná soustava ve většině aplikací nevyhovuje, jejímu předefinování se budeme věnovat později.