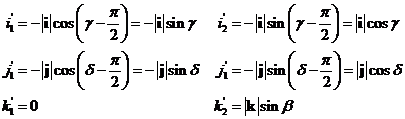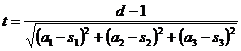Promítání
prostoru na rovinu
Rovnoběžné
promítání
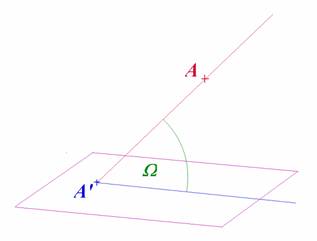
Promítací paprsky svírají při tomto promítání s
půmětnou úhel  obecně různý od
obecně různý od 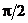 . Jedná se o zobrazení
. Jedná se o zobrazení 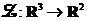 .
.
Poznámka: v následujícím budeme
písmenem 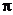 označovat
axonometrickou průmětnu tak, jak je to obvyklé v konstruktivní geometrii.
označovat
axonometrickou průmětnu tak, jak je to obvyklé v konstruktivní geometrii.
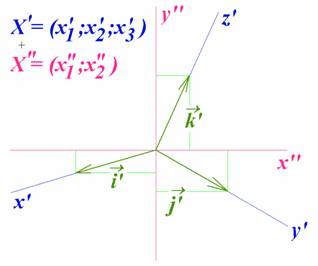
V tomto zobrazení se („prostorové“) osy 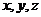 souřadné soustavy
souřadné soustavy
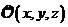 zobrazí na trojici přímek
zobrazí na trojici přímek 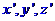 v rovině
v rovině 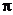 , jednotkové vektory
, jednotkové vektory 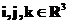 na vektory
na vektory 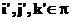 . Ztotožníme-li tedy průmětnu
. Ztotožníme-li tedy průmětnu 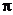 s nákresnou
(obrazovkou počítače), dostaneme situaci na dalším obrázku. Aby trojice přímek
v rovině mohla být považována za průmět souřadné soustavy v kosoúhlé‚
axonometrii, je třeba kromě společného průsečíku požadovat jen to, aby žádné
dvě nesplývaly. Průmětnu
s nákresnou
(obrazovkou počítače), dostaneme situaci na dalším obrázku. Aby trojice přímek
v rovině mohla být považována za průmět souřadné soustavy v kosoúhlé‚
axonometrii, je třeba kromě společného průsečíku požadovat jen to, aby žádné
dvě nesplývaly. Průmětnu 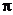 opatříme souřadnou
soustavou
opatříme souřadnou
soustavou 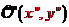 dle připojeného
obrázku. Jedná se o stejnou uživatelskou souřadnou soustavu, kterou jsme
používali v unitě GRAPH2D. Vektory
dle připojeného
obrázku. Jedná se o stejnou uživatelskou souřadnou soustavu, kterou jsme
používali v unitě GRAPH2D. Vektory 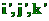 nechť mají v této souřadné soustavě
souřadnice
nechť mají v této souřadné soustavě
souřadnice 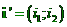 ,
, 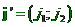 ,
, 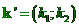 Zobrazení,
které zobrazuje libovolný bod
Zobrazení,
které zobrazuje libovolný bod 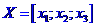 na bod
na bod 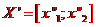 je dáno rovnicemi
je dáno rovnicemi
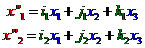
Tyto dvě rovnice jsou základem unity GRAPH3D: Procedure Projection
(X:T3DPoint;var Xp:T2DPoint), která umožňuje 3D modelování. Tato procedura promítá „prostorový“ bod
typu T3DPoint jeho průmět v rovině typu T2DPoint. Všechny procedury
sestrojující prostorové objekty pak jednotlivé body „prohánějí“ touto
procedurou. Například procedura pro konstrukci úsečky v prostoru vypadá
takto:
procedure
TDraw3D.Line(A,B:T3DPoint;Red,Green,Blue:Byte);
var Xp,Yp:T2DPoint;
begin
Projection(A,Xp);Projection(B,Yp);
With
Image1.Canvas do{pro kreslení do objektu Canvas}
begin
Pen.Color:= Red+256*Green+256*256*Blue;
MoveTo(XCoor(Xp[1]),YCoor(Xp[2]));
LineTo(XCoor(Yp[1]),YCoor(Yp[2]));
end;
//X[1]:=XCoor(pX[1]);X[2]:=YCoor(pX[2]);
{přímým přístupem do ScanLine}
//Y[1]:=XCoor(pY[1]);Y[2]:=YCoor(pY[2]);
Line2D(X,Y,Red,Green,Blue);
end;

Poznámky:
1. Všimněte si, že v GRAPH3D
jsou body deklarovány jako čtyřsložkové pole. Důvod je analogický jako v
GRAPH2D (třísložkové‚ pole). Je to kvůli transformacím v prostoru, kterými se
budeme zabývat později.
2. Jednotka GRAPH3D připojená
k tomuto příkladu obsahuje jen několik procedur nutných speciálně k této
kunstrukci. Podstatně bohatší stejnojmenná jednotka se nachází v podadresáři
UNITS. Její jednotlivé procedury budeme postupně probírat, a to v této a
několika následujících kapitolách.
3. Konstrukce jsou prozatím
prováděny do objektu Canvas obrazu Image1. Poněkud pomalejší vykreslování
prozatím nevadí. V závorce uvedený přístup do ScanLine předpokládá navíc
deklaraci proměnných X, Y jako TPixel (stačí lokální). Uvedená procedura Line2D
je totožná s „dvojrozměrnou úsečkou“ v GRAPH2D.
Příklad
1:
Zobrazení krychle v libovolném rovnoběžném promítání. Protože krychle je jedno
z nejjednodušších těles a budeme ho často používat, napíšeme si v GRAPH3D
proceduru Box_LineModel, což je procedura, která spojí příslušné‚ vrcholy
hranami. Protože nám zadání poskytuje volnost v poloze krychle i volbě
parametrů axonometrie, je krychle umístěna tak, že tři její hrany leží v
souřadných osách a parametry axonometrie jsou voleny libovolně. Je zřejmé, že
volbou j2'=0, k1'=0
dostaneme tzv. volné rovnoběžné promítání .
Zde najdete kompletní
zdrojový kód
a
zde spustitelný
kód
Hranové
konstrukce ploch
Nejdříve si všimněme konstrukcí ploch zadaných ve
tvaru 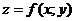 Tyto plochy
sestrojujeme pomocí procedury PolyLine, která tentokrát pracuje ve
Tyto plochy
sestrojujeme pomocí procedury PolyLine, která tentokrát pracuje ve 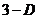 . Jejími parametry je pole
. Jejími parametry je pole 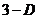 bodů, kterými má
křivka procházet,
bodů, kterými má
křivka procházet, 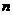 počet bodů a barevné složky Red, Green, Blue.
Plochu sestrojíme pomocí řezů rovinami kolmými na osu
počet bodů a barevné složky Red, Green, Blue.
Plochu sestrojíme pomocí řezů rovinami kolmými na osu 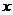 , resp
, resp 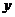 . Řez kolmý např. na osu
. Řez kolmý např. na osu 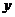 sestrojíme tak, že první souřadnice bodů každé křivky
naplníme hodnotami
sestrojíme tak, že první souřadnice bodů každé křivky
naplníme hodnotami 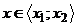 , druhá je konstantní. Výsledkem cyklického volání procedury
přes interval
, druhá je konstantní. Výsledkem cyklického volání procedury
přes interval 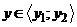 je osnova zelených
řezů na přiloženém obrázku. V programové realizaci to znamená, že cyklus
pro
je osnova zelených
řezů na přiloženém obrázku. V programové realizaci to znamená, že cyklus
pro  bude vnější, pro
bude vnější, pro 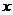 vnitřní
vnitřní

Příklad
1: Hranová
konstrukce plochy 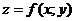 :
:
hx:=(x2-x1)/40;hy:=(y2-y1)/40;
y:=y1;
Repeat
x:=x1;i:=0;
Repeat
i:=succ(i);
A[i,1]:=x;A[i,2]:=y;A[i,3]:=f(x,y);x:=x+hx;
until x>x2;
Draw3D.PolyLine(A,i,Red,Green,Blue);
y:=y+hy;
until y>y2;
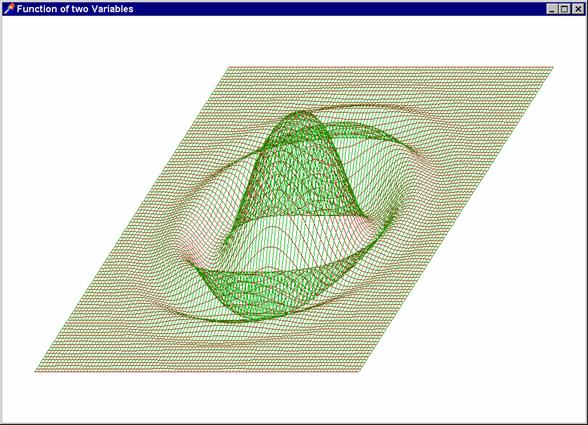
Přehozením cyklů získáme osnovu řezů kolmých na osu
x (vykresleno červeně).
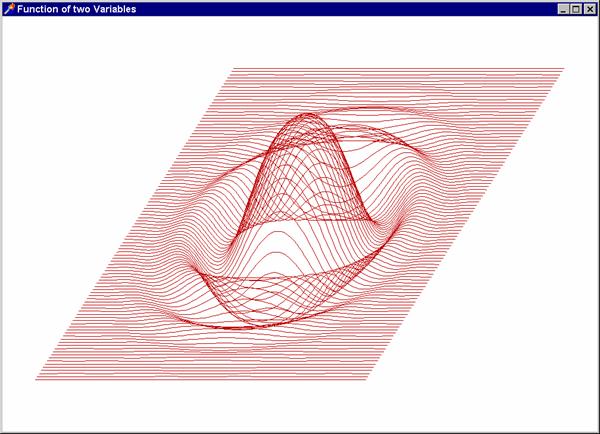
Z těchto dvou osnov křivek sestrojíme model grafu
funkce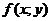 nad obdélníkem
nad obdélníkem 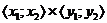 . (Podélné a příčné řezy jsou zde barevně rozlišeny
z demonstračních důvodů. Obvykle se sestrojují stejnou barvou). Na
připojených obrázcích je graf funkce
. (Podélné a příčné řezy jsou zde barevně rozlišeny
z demonstračních důvodů. Obvykle se sestrojují stejnou barvou). Na
připojených obrázcích je graf funkce 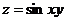 nad obdélníkem
nad obdélníkem 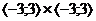 ve volném rovnoběžném
promítání.
ve volném rovnoběžném
promítání.
Zde najdete kompletní
zdrojový kód
a
zde
spustitelný
kód
Příklad
2: Umožňuje
uživateli zadat rovnici funkce za běhu programu.
Zde najdete kompletní
zdrojový kód
a
zde
spustitelný
kód
Je-li plocha zadána parametrickými rovnicemi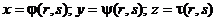 , je postup analogický. Cyklováním přes parametr
, je postup analogický. Cyklováním přes parametr 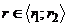 dostaneme první osnovu
křivek, cyklováním přes
dostaneme první osnovu
křivek, cyklováním přes 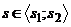 , pak druhou.
, pak druhou.
Příklad
3:
Vykreslete anuloid, kulovou a válcovou plochu ve volném rovnoběžném promítání a
ověřte známé vlastnosti těchto průmětů (elipsovitý průmět kulové plochy, sklon
hlavní poloosy průmětu kružnice...).
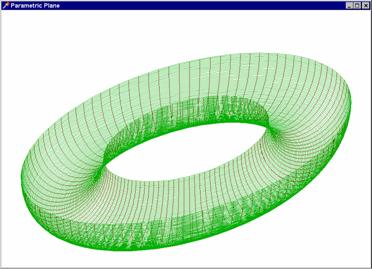
Program, jehož zdrojový
kód najdete zde a spustitelný
kód zde, vykresluje anuloid v kosoúhlé axonometrii.
Program, jehož zdrojový
kód najdete zde a spustitelný
kód zde, je upraven tak, že uživatel má opět možnost zadávat rovnici plochy
za běhu programu.
Nejméně příjemným zadáním je pro programátora plocha
určená rovnicí 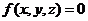 . Tuto konstrukci nelze provést pomocí kolmých řezů, které
jsme použili výše. Plochu je třeba vhodně segmentovat. Postup je trojrozměrným
zobecněním konstrukce křivek zadaných rovnicí
. Tuto konstrukci nelze provést pomocí kolmých řezů, které
jsme použili výše. Plochu je třeba vhodně segmentovat. Postup je trojrozměrným
zobecněním konstrukce křivek zadaných rovnicí
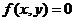 , která byla uvedena v kpt. 3.4. Konstrukce ploch určených
rovnicí
, která byla uvedena v kpt. 3.4. Konstrukce ploch určených
rovnicí 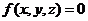 bude uvedena v kpt.
8.2.
bude uvedena v kpt.
8.2.
Pravoúhlé
promítání
Kosoúhlé promítání není příliš vhodná pro konstrukce
obektů, které mají simulovat pohled na reálný předmět. Srovnání kosoúhlého
kolmého promítání vidíme na připojeném obrázku. Známým modelem kosoúhlého
promítání je vrhání stínů slunečními paprsky na rovinnou podložku. Pohled na
drátěný model tělesa představuje axonometrii kolmou, pohled na jeho stín pak
axonometrii kosoúhlou. Čím je Slunce níž nad obzorem, tím jsou stíny-kosoúhlé
průměty protaženější. Reálný zrakový vjem vzniká tak, že světelné paprsky
odražené vnímaným objektem procházejí zorničkou oka a dopadají kolmo na jeho
sítnici. Je-li zorný úhel, pod kterým předmět pozorujeme, dostatečně malý, lze
paprsky považovat za rovnoběžku a sítnici oka za rovinu. Má-li tedy
sestrojovaný průmět nahrazovat pohled na reálný předmět, je třeba použít
pravoúhlé promítání.
Lineární transformace, která zobrazuje libovolný bod
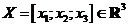 na bod
na bod 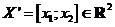 je dána rovnicemi
je dána rovnicemi
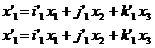
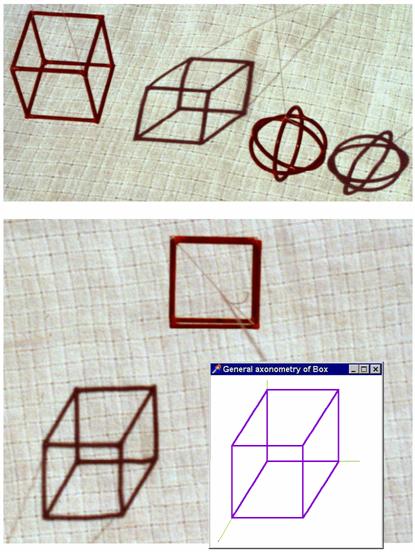
Nyní je třeba určit koeficienty 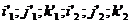 tak, aby tato
transformace byla pravoúhlým promítáním. Uživatel grafického systému obvykle
volí „směr pohledu“, tj. směr promítání, a to pomocí horizontálního úhlu a a vertikálního úhlu b. Označíme-li pořadě
tak, aby tato
transformace byla pravoúhlým promítáním. Uživatel grafického systému obvykle
volí „směr pohledu“, tj. směr promítání, a to pomocí horizontálního úhlu a a vertikálního úhlu b. Označíme-li pořadě 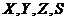 průsečíky průmětny se
souřadnými osami, resp. s promítacím paprskem, který prochází počátkem, pak
platí:
průsečíky průmětny se
souřadnými osami, resp. s promítacím paprskem, který prochází počátkem, pak
platí:
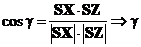
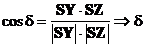
kde g, d úhly mezi průměty souřadných os (viz
obrázek) a dále je
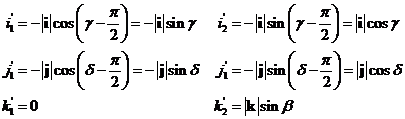
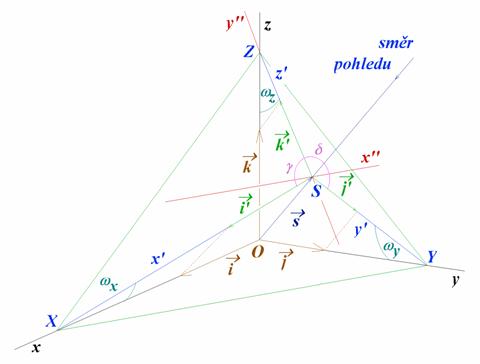
Tyto vzorce jsou součástí procedury SetOrthoAxonProjection,
která pro hodnoty úhlů a, b definujících směr pohledu do souřadné
soustavy nastavuje průměty 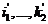 .
.
Úlohy,
které jsme výše řešili v rovnoběžném promítání jsou nyní řešeny v promítání
kolmém:
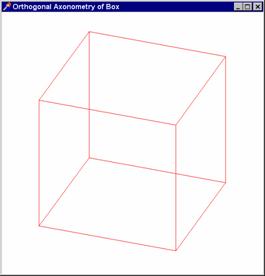

Zobrazení
krychle
zdrojový
kód spustitelný
kód
Graf
funkce dvou proměnných
zdrojový kód spustitelný
kód
(totéž
s interaktivní změnou rovnice plochy) zdrojový
kód spustitelný
kód
Plocha
zadaná parametrickými rovnicemi zdrojový
kód spustitelný
kód
(totéž
s interaktivní změnou rovnic plochy) zdrojový
kód spustitelný
kód
Středové
promítání
Pozorujeme-li reálné objekty pod větším zorným
úhlem, je třeba při jejich zobrazování použít středové promítání na rovinu.
Kolmici spuštěnou se středu promítání na průmětnu nazýváme hlavní paprsek.
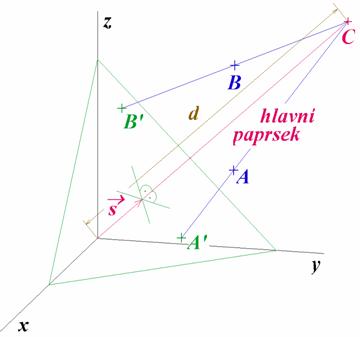
Při programovém zpracování středového promítání
vyzžijeme algoritmů z předchozí kapitoly. Konstrukci průmětů budeme řešit
procedurou SetCenterProjection.
Do ní můžeme převzít všechny procedury SetOrthoAxonProjection, které pouze doplníme.
Především opět určíme směr pohledu do souřadné soustavy  . Zvolený horizontální a vertikální úhel bude nyní
určovat směr tzv. hlavního paprsku, tj. promítacího paprsku kolmého na
průmětnu. Tento směr budeme opět reprezentovat jednotkovým směrovým vektorem
. Zvolený horizontální a vertikální úhel bude nyní
určovat směr tzv. hlavního paprsku, tj. promítacího paprsku kolmého na
průmětnu. Tento směr budeme opět reprezentovat jednotkovým směrovým vektorem  , který je tedy určen souřadnicemi
, který je tedy určen souřadnicemi
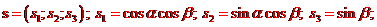
Průmětnu určíme podobně jako v předchozí
kapitole - je kolmá na hlavní paprsek a zvolíme ji v jednotkové
vzdálenosti od počátku. Střed  promítání (ObserverPoint) určíme zadáním vzdálenosti
promítání (ObserverPoint) určíme zadáním vzdálenosti  pozorovatele od
počátku. Jeho souřadnice pak zjistíme snadno jako
pozorovatele od
počátku. Jeho souřadnice pak zjistíme snadno jako 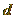 -násobek (ObserverDistance)
souřadnic směrového vektoru (předpokládáme zadávání úhlů a, b ve stupních):
-násobek (ObserverDistance)
souřadnic směrového vektoru (předpokládáme zadávání úhlů a, b ve stupních):
ObserverPoint[1]:=ObserverDistance*cos(Alfa*pi/180)*cos(Beta*pi/180);
ObserverPoint[2]:=ObserverDistance*sin(Alfa*pi/180)*cos(Beta*pi/180);
ObserverPoint[3]:=ObserverDistance*sin(Beta*pi/180);
Průmět 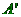 bodu
bodu 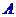 určíme jako průsečík přímky
určíme jako průsečík přímky  s průmětnou. Průmětna má rovnici
s průmětnou. Průmětna má rovnici 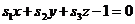 , parametrické rovnice promítacího paprsku jsou
, parametrické rovnice promítacího paprsku jsou
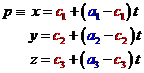
Dosazením do rovnice průmětny dostáváme pro hodnot
parametru rovnici
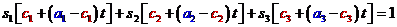
Odtud máme hodnotu parametru: 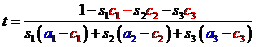
Tento vzoreček je použit v následující proceduře
(střed promítání C je označen ObserverPoint - bod pozorování):
Procedure TDraw3D.PlaneIntersect(A:T3DPoint;var
pA:T3DPoint);
var t:Double;
S:TVector;
begin
S:=MajorRay;
t:=1-S[1]*ObserverPoint[1]-S[2]*ObserverPoint[2]-S[3]*ObserverPoint[3];
t:=t/(S[1]*(A[1]-ObserverPoint[1])+S[2]*(A[2]-ObserverPoint[2])+S[3]*(A[3]-ObserverPoint[3]));
pA[1]:=ObserverPoint[1]+(A[1]-ObserverPoint[1])*t;
pA[2]:=ObserverPoint[2]+(A[2]-ObserverPoint[2])*t;
pA[3]:=ObserverPoint[3]+(A[3]-ObserverPoint[3])*t;
end;
Tento průsečík se nachází v průmětně, která
splývá s obrazovkou, a je třeba ho ještě transformovat do světových
souřadnic procedurou Projection. Tyto dvě procedury je pak třeba použít při
každém nastavování bodu. Např. procedura pro kreslení úsečky vypadá takto
(čtenář nechť tuto proceduru srovná se stejnou procedurou v kapitole
3.1.):
procedure
Draw3D.Line(A,B:T3DPoint;Red,Green,Blue:Byte);
var
Xp,Yp :T2DPoint;
Xc,Yc :T3DPoint;
begin
PlaneIntersect(A,Xc);PlaneIntersect(B,Yc);
Projection(Xc,Xp);Projection(Yc,Yp);
{pro kreslení do objektu Canvas}
With
Image1.Canvas do
begin
Pen.Color:=Red+256*Green+256*256*Blue;
MoveTo(XCoor(Xp[1]),YCoor(Xp[2]));
LineTo(XCoor(Yp[1]),YCoor(Yp[2]));
end;
{přímým
přístupem do ScanLine
X[1]:=XCoor(pX[1]);X[2]:=YCoor(pX[2]);Y[1]:=XCoor(pY[1]);Y[2]:=YCoor(pY[2]);
Line2D(X,Y,Red,Green,Blue);}
Zobrazování
objektů ve středovém promítání:
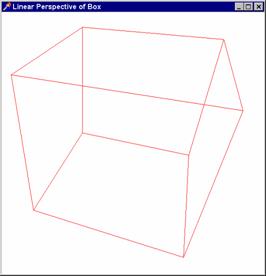
Zobrazení
krychle
zdrojový
kód spustitelný
kód
Graf
funkce dvou proměnných
zdrojový kód spustitelný
kód
(totéž s interaktivní změnou rovnice plochy) zdrojový
kód spustitelný
kód
Plocha
zadaná parametrickými rovnicemi zdrojový kód spustitelný
kód
(totéž s interaktivní změnou rovnic plochy) zdrojový
kód spustitelný
kód
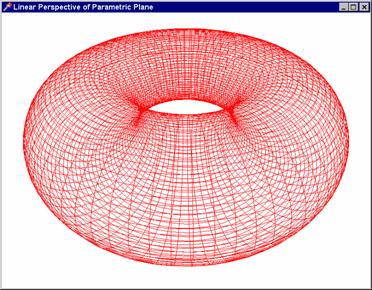
Poznámka: Tvar průmětů prostorových
útvarů závisí na relativní vzdálenosti středu promítání od promítaného útvaru,
přesněji řečeno na maximálním úhlu, který svírají promítací paprsky (tzv.
zorném úhlu). Zorný úhel člověka je individuální a pohybuje se mezi 42 -
44 stupni. Tomuto zornému úhlu odpovídá obrázek grafu funkce 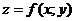 . Krychli ani anuloid tak, jak jsou zobrazeny, by již člověk
vidět nemohl. Zorný úhel krychle je asi 60o, anuloidu dokonce 67o
. Takto zobrazit tato tělesa dokáže jen počítač nebo širokoúhlý objektiv.
. Krychli ani anuloid tak, jak jsou zobrazeny, by již člověk
vidět nemohl. Zorný úhel krychle je asi 60o, anuloidu dokonce 67o
. Takto zobrazit tato tělesa dokáže jen počítač nebo širokoúhlý objektiv.


Ještě extrémnější příklad vidíme na tomto obrázku. Vlevo
- snímek pořízený širokoúhlým objektivem Canon. Promítací paprsek dopadá na
silnici v dolní části obrázku téměř kolmo, v horní části snímku je s
ní téměř rovnoběžný. Z toho vyplývá, že zorný úhel tohoto objektivu je
téměř 90o. Vpravo vidíme prakticky stejnou (i když značně
zjednodušenou) scénu sestrojenou počítačem
Promítání
na kulovou plochu
Dosud jsme se zabývali promítáním prostoru na
rovinu. V praxi se však často vyskytují případy, kdy je při promítání
zapotřebí velmi velký zorný úhel. V těchto případech přestává promítání na
rovinu vyhovovat, neboť rozměry průmětny extrémně rostou. Existují dokonce
objektivy se zorným úhlem větším než 180o a promítání na
rovinu není možné z principu. V těchto případech lze použít promítání
na kulovou nebo válcovou plochu. Zde existuje více možností volby průmětny, tak
způsobu transformace z kulové či válcové plochy do roviny, ke které
v konečné fázi musí dojít. V tomto odstavci ukážeme jednu z možností,
při které využijeme předcházejících výsledků. Převezmeme střed
promítání, jeho určení směrovými úhly a jeho vzdáleností od počátku
souřadné soustavy. Převezmeme také promítací rovinu splývající s rovinou
obrazovky. Promítacímu paprsku však postavíme do cesty kulovou plochu, jejíž
středem bude střed promítání a která se bude této roviny dotýkat. Bod 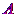 promítneme středově na kulovou plochu do bodu
promítneme středově na kulovou plochu do bodu 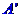 , tento bod pak komým promítáním do roviny výstupního
zařízení (bod
, tento bod pak komým promítáním do roviny výstupního
zařízení (bod 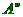 ).
).
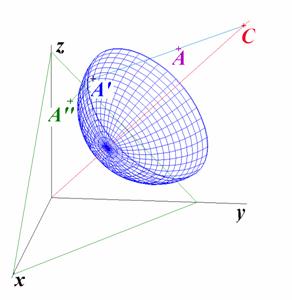
V algoritmickém zpracování průmětu bodu tak
dojde oproti předchozí kapitole k jediné změně: procedurou Intersect
určujeme průsečík nikoli se zelenou rovinou, ale s modrou kulovou plochou.
Promítací paprsek je stejně jako v předchozím případě určen bodem  a směrovým
vektorem
a směrovým
vektorem  . Průsečík s kulovou plochou
. Průsečík s kulovou plochou 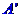 je na této
přímce tentokrát určen hodnotou parametru
je na této
přímce tentokrát určen hodnotou parametru
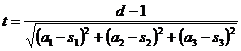
Nastavení tohoto parametru je to
jediné, v čem se promítání bodu na kulovou plochu liší od promítání na rovinu. Při
promítání úseček však musíme mít na paměti, že díky tomuto nastavení parametru
se jedná o transformaci nelineární (úsečka se promítne do kruhového
oblouku). Průmět úsečky je tedy třeba konstruovat jako křivku pomocí jejích
parametrických rovnic (viz př. 2 v kpt.6.1.).
Příklad
1.: Zde je
zpracován průmět krychle na kulovou plochu
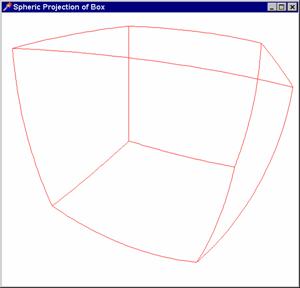
Zde najdete kompletní
zdrojový kód
a
zde spustitelný
kód
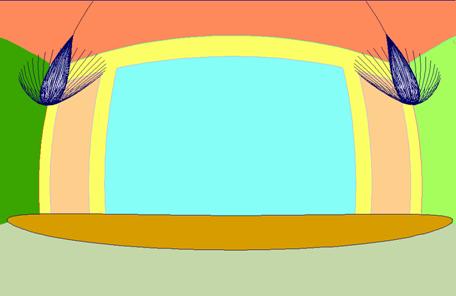
Na připojeném obrázku vidíte snímek místnosti
pořízený objektivem s velmi velkým zorným úhlem („rybím okem“). Zorný úhel
tohoto objektivu se blíží 180o. Na dalším obrázku máme prakticky
stejnou (pouze zjednodušenou) scénu sestrojenou počítačem.

![]() obecně různý od
obecně různý od ![]() . Jedná se o zobrazení
. Jedná se o zobrazení ![]() .
.

![]() označovat
axonometrickou průmětnu tak, jak je to obvyklé v konstruktivní geometrii.
označovat
axonometrickou průmětnu tak, jak je to obvyklé v konstruktivní geometrii.![]() souřadné soustavy
souřadné soustavy
![]() zobrazí na trojici přímek
zobrazí na trojici přímek ![]() v rovině
v rovině ![]() , jednotkové vektory
, jednotkové vektory ![]() na vektory
na vektory ![]() . Ztotožníme-li tedy průmětnu
. Ztotožníme-li tedy průmětnu ![]() s nákresnou
(obrazovkou počítače), dostaneme situaci na dalším obrázku. Aby trojice přímek
v rovině mohla být považována za průmět souřadné soustavy v kosoúhlé‚
axonometrii, je třeba kromě společného průsečíku požadovat jen to, aby žádné
dvě nesplývaly. Průmětnu
s nákresnou
(obrazovkou počítače), dostaneme situaci na dalším obrázku. Aby trojice přímek
v rovině mohla být považována za průmět souřadné soustavy v kosoúhlé‚
axonometrii, je třeba kromě společného průsečíku požadovat jen to, aby žádné
dvě nesplývaly. Průmětnu ![]() opatříme souřadnou
soustavou
opatříme souřadnou
soustavou ![]() dle připojeného
obrázku. Jedná se o stejnou uživatelskou souřadnou soustavu, kterou jsme
používali v unitě GRAPH2D. Vektory
dle připojeného
obrázku. Jedná se o stejnou uživatelskou souřadnou soustavu, kterou jsme
používali v unitě GRAPH2D. Vektory ![]() nechť mají v této souřadné soustavě
souřadnice
nechť mají v této souřadné soustavě
souřadnice ![]() ,
, ![]() ,
, ![]() Zobrazení,
které zobrazuje libovolný bod
Zobrazení,
které zobrazuje libovolný bod ![]() na bod
na bod ![]() je dáno rovnicemi
je dáno rovnicemi![]()

![]() Tyto plochy
sestrojujeme pomocí procedury PolyLine, která tentokrát pracuje ve
Tyto plochy
sestrojujeme pomocí procedury PolyLine, která tentokrát pracuje ve ![]() . Jejími parametry je pole
. Jejími parametry je pole ![]() bodů, kterými má
křivka procházet,
bodů, kterými má
křivka procházet, ![]() počet bodů a barevné složky Red, Green, Blue.
Plochu sestrojíme pomocí řezů rovinami kolmými na osu
počet bodů a barevné složky Red, Green, Blue.
Plochu sestrojíme pomocí řezů rovinami kolmými na osu ![]() , resp
, resp ![]() . Řez kolmý např. na osu
. Řez kolmý např. na osu ![]() sestrojíme tak, že první souřadnice bodů každé křivky
naplníme hodnotami
sestrojíme tak, že první souřadnice bodů každé křivky
naplníme hodnotami ![]() , druhá je konstantní. Výsledkem cyklického volání procedury
přes interval
, druhá je konstantní. Výsledkem cyklického volání procedury
přes interval ![]() je osnova zelených
řezů na přiloženém obrázku. V programové realizaci to znamená, že cyklus
pro
je osnova zelených
řezů na přiloženém obrázku. V programové realizaci to znamená, že cyklus
pro ![]() bude vnější, pro
bude vnější, pro ![]() vnitřní
vnitřní
![]() :
:
![]() nad obdélníkem
nad obdélníkem ![]() . (Podélné a příčné řezy jsou zde barevně rozlišeny
z demonstračních důvodů. Obvykle se sestrojují stejnou barvou). Na
připojených obrázcích je graf funkce
. (Podélné a příčné řezy jsou zde barevně rozlišeny
z demonstračních důvodů. Obvykle se sestrojují stejnou barvou). Na
připojených obrázcích je graf funkce ![]() nad obdélníkem
nad obdélníkem ![]() ve volném rovnoběžném
promítání.
ve volném rovnoběžném
promítání.