Technické plochy
Bézierovy
plochy
Bézierovy plochy stejně jako plochy Fergusonovy a Coonsovy, kterými se budeme zabývat dále, patří mezi tzv. technické plochy. Motivy, které vedly k rozvoji teorie těchto ploch, jsou charakterizovány snahou oprostit uživatele grafických systémů od matematiky a úsilím o maximální geometrickou názornost. Uživatel modeluje plochu tak, že většinou zadává „řídící body“ (např. rohy), okrajové křivky, tečné vektory apod.
Bézierova bikubická plocha: je dvojrozměrným zobecněním Bézierovy kubiky. Její parametrické rovnice vyjádříme v maticové podobě:
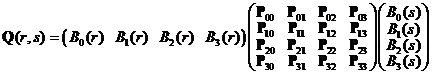
kde polynomy ![]() známe již
z Bézierovy kubiky, pro parametry je
známe již
z Bézierovy kubiky, pro parametry je ![]() a body
a body ![]() jsou řídící body
plochy. Ty tvoří tzv. řídící polygon, pomocí něhož plochu tvarujeme (na
připojeném obrázku vyznačen červeně, resp. zeleně).
jsou řídící body
plochy. Ty tvoří tzv. řídící polygon, pomocí něhož plochu tvarujeme (na
připojeném obrázku vyznačen červeně, resp. zeleně).
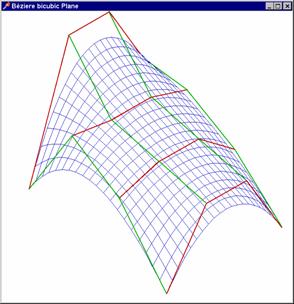
Dá se dokázat (a z obrázku
je také patrné), že hrany řídícího polygonu vycházející z bodů ![]() jsou tečny plochy ve směru
souřadných os a že okraje plochy jsou tvořeny Bézierovými kubikami.
jsou tečny plochy ve směru
souřadných os a že okraje plochy jsou tvořeny Bézierovými kubikami.
Příklad 1.: Naprogramujme konstrukci Bézierovy bikubické plochy.
Pro tyto účely bude vhodnější
vyjádřit rovnici plochy trochu jinak. Jestliže bychom začali výše uvedený
maticový zápis roznásobovat, je zřejmé, že bod ![]() plochy dostaneme jako součet
plochy dostaneme jako součet
![]()
Tento součet je třeba
rozepsat v jednotlivých souřadnicích. Sestavme tedy proceduru BezierePlane
(vzhledem k tomu, že k rozlišení bodů řídícího polygonu je zapotřebí
dvou indexů, jejich
jednotlivé souřadnice již nebudeme rozlišovat indexem, ale písmenem).
procedureTDraw3D.BezierePlane(Sender:TObject);
type
TPointOfGrid = record x,y,z:Double;end;
TGrid=array [0..3,0..3] of TPointOfGrid;
{Deklarujme typ TPointOfGrid jako}
var P:TGrid; {záznam tří
reálných souřadnic a TGrid jako dvojrozměrné pole - matici}
i,j :Integer;
{těchto záznamů}
Alfa,Beta:Double;
{pohledové úhly}
Protože polynomy ![]() (tzv. Bernsteinovy polynomy se liší podle
indexu i, naprogramujeme si jejich vyčíslování jako funkci:
(tzv. Bernsteinovy polynomy se liší podle
indexu i, naprogramujeme si jejich vyčíslování jako funkci:
Function
B(i:Integer;t:Double):Double;
begin
Case i of
0:B:=(1-t)*(1-t)*(1-t); 1:B:=3*t*(1-t)*(1-t);
2:B:=3*t*t*(1-t);
3:B:=t*t*t;
end;
end;
Samotný součet pak můžeme počítat procedurou Bezi:
Procedure
Bezi(r,s:Real;var A:T3DPoint);
var i,j:Integer;
begin
A[1]:=0;
for i:=0 to 3 do
for j:=0 to 3 do
A[1]:=A[1]+P[i,j].X*B(i,r)*B(j,s);
A[2]:=0;
for i:=0 to 3 do
for j:=0 to 3 do
A[2]:=A[2]+P[i,j].Y*B(i,r)*B(j,s);
A[3]:=0;
for i:=0 to 3 do
for j:=0 to 3 do
A[3]:=A[3]+P[i,j].Z*B(i,r)*B(j,s);
end;
Konstrukce
sítě řídících bodů a samotné plochy pak vypadá následovně:
begin
x1:=-230;x2:=240;y1:=-300;
With Image1 do
y2:=y1+(x2-x1)*Height/Width;
Scale(x1,x2,y1,y2);Alfa:=40;Beta:=30;
View(Alfa,Beta);
{****
definice řídícího polygonu ******}
P[0,0].X:=
10;P[0,0].Y:= 10;P[0,0].Z:= 150;
...........................................
P[3,3].X:=300;P[3,3].Y:=300;P[3,3].Z:=-100;
for i:=0 to 3 do {„červená“ část polygonu}
begin
for j:=0 to 3 do
begin Q[j,1]:=P[i,j].X;Q[j,2]:=P[i,j].Y;Q[j,3]:=P[i,j].Z; end;
PolyLine(Q,4,255,0,0)
end;
for i:=0 to 3 do
{„zelená“ část polygonu}
begin
for j:=0 to 3 do
begin
Q[j,1]:=P[j,i].X;Q[j,2]:=P[j,i].Y;Q[j,3]:=P[j,i].Z;
end;
PolyLine(Q,4,0,255,0)
end;
end;
hr:=0.1;hs:=0.1; r:=0; {konstrukce samotné plochy - podélné řezy}
While r<=1+hr do
begin
s:=-hs;i:=0;
While s<=1+hs do
begin Bezi(r,s,C[i]);i:=succ(i);s:=s+hs;end;
PolyLine(C,i-1,0,0,200);r:=r+hr;
end;
................. {příčné řezy analogicky přehozením cyklů}
end;
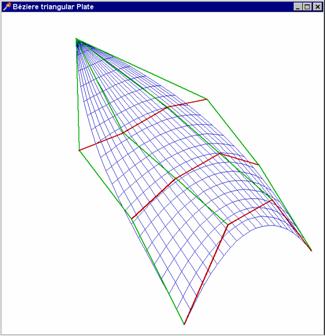
Výstup z tohoto programu jsme viděli výše. Jestliže řídící polygon
zadáme tak, že ztotožníme body na některém jeho okraji, přejde tento okraj
v bod a dostáváme plochu „trojúhelníkovou“, jak je
opět patrné z připojeného
obrázku.
Zde najdete kompletní zdrojový kód
a
zde spustitelný kód
Jednou z výhod těchto technických ploch je jednoduchost sestavování
velkých ploch z jednotlivých „plátů“. Technická praxe
většinou vyžaduje napojování hladké, tj. takové, aby výsledná plocha byla
spojitá i se svými minimálně prvními parciálními derivacemi.
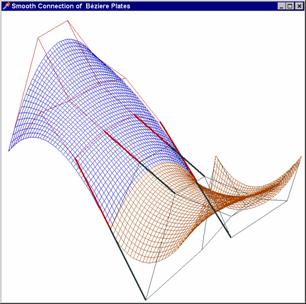
U Bézierových ploch lze toto podmínku splnit velmi jednoduše. Okraj, na
který chceme napojovat, musí být samozřejmě společný, což zařídíme společným
okrajem řídícího polygonu. Příčné hrany sousedních polygonů (vyznačené silně)
pak musí ležet na téže přímce. Tato podmínka je zřejmá především
u okrajových hran, které musí tvořit společnou tečnu obou plátů.
Nejjednodušeji tuto podmínku splníme tak, že nové krajní body zadáme středově
souměrné se „starými“ podle bodů společného okraje.
Příklad 2.: Naprogramujme hladké spojení
dvou Bézierových plátů.
Zadávání nového polygonu pomocí
polygonu starého pak může v programu vypadat např. takto:
for i:=0 to 3 do
begin
P[0,i]:=P[3,i]; {předefinování
„staré čtvrté řady“ na „první novou“}
P[1,i].X:=2*P[0,i].X-P[2,i].X;
{nastavení x, y, z tové souřadnice bodu v „nové druhé řadě“ }
P[1,i].Y:=2*P[0,i].Y-P[2,i].Y;
{středově souměrně s toutéž souřadnicí ve „staré třetí řadě“}
P[1,i].Z:=2*P[0,i].Z-P[2,i].Z;
end;
V „novém“ polygonu nyní zbývá
nastavit třetí a čtvrtou řadu bodů a opakovat konstrukci plochy.
Protože nyní sestrojujeme pláty dva, je z úsporných důvodů celá konstrukce
řídícího polygonu a následně i plátu vyvedena do samostatné procedury
s názvem BeziPlate s celkem šesti parametry typu byte. První tři
definují barvu, kterou má být sestrojen polygon, druhá trojice pak barvu
samotné plochy.
Zde najdete kompletní zdrojový kód
a
zde
spustitelný kód
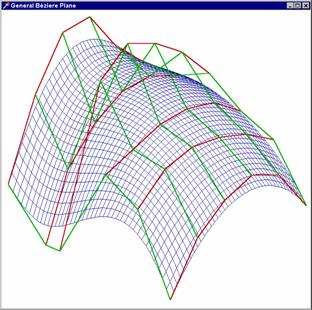
Obecná Bezierova plocha: vznikne
zobecněním Bezierovy bikubické plochy. Její rovnici
obdržíme z rovnice (1) tím, že matici řídících bodů ![]() typu 4´4
nahradíme maticí typu m´n,
n; m³4
a speciální kubické
Bernsteinovy polynomy nahradíme polynomy obecnými - viz. kpt.
3.9., příklad 3. Pro implementaci na počítači je opět výhodnější rovnice
typu 4´4
nahradíme maticí typu m´n,
n; m³4
a speciální kubické
Bernsteinovy polynomy nahradíme polynomy obecnými - viz. kpt.
3.9., příklad 3. Pro implementaci na počítači je opět výhodnější rovnice
![]()
Toto zobecnění není příliš
složité a je zcela analogické postupu v jednorozměrném případě,
uvedeném v kapitole 3.9., proto se jím nebudu dále zabývat. Výstup si
můžeme prohlédnout na připojeném obrázku.
Zde najdete kompletní zdrojový kód
a zde spustitelný kód
Racionální Bezierova plocha: je 3-D
zobecněním racionální Bezierovy křivky. Plocha je určena rovnicí
![]() , kde
, kde 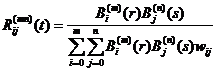
a ![]() jsou váhy
přiřazené jednotlivým řídícím bodům. Implementaci lze provést následujícím
způsobem:
jsou váhy
přiřazené jednotlivým řídícím bodům. Implementaci lze provést následujícím
způsobem:
Function RatioBezi(i,j:Integer;r,s:Double) :Double;
var
k,l:Integer;Value:Double;
begin
Value:=0;
For k:=0 to m do
For l:=0 to n do Value:=Value+B(k,r)*B(l,s)*w[k,l];
RatioBeziere:=
B(i,r)*B(j,s)*w[i,j]/Value;
end;
ProcedureBezierePlane(r,s:Double;
var A:T3DPoint);
var i,j:Integer;
begin
A[1]:=0;A[2]:=0;A[3]:=0;
for i:=0 to m do for j:=0 to n do
begin
A[1]:=A[1]+P[i,j].X*RatioBezi(i,j,r,s);
A[2]:=A[2]+P[i,j].Y*RatioBezi(i,j,r,s);
A[3]:=A[3]+P[i,j].Z*RatioBezi(i,j,r,s);
end;
end;
V programu je pak třeba
deklarovat a naplnit matici ![]() váhových koeficientů, procedura BeziPlane pak
pro jednotlivé hodnoty parametrů
váhových koeficientů, procedura BeziPlane pak
pro jednotlivé hodnoty parametrů ![]() generuje body Bézierovy racionální
plochy. Váhy mají analogický význam jako v jednorozměrném případě. Jejich
velikost určuje vzdálenost plochy od příslušných řídících bodů. Jsou-li všechny
váhy rovny jedné, dostáváme „klasickou“ Bézierovu plochu. V řešeném příkladu
zadává uživatel váhové koeficienty pomocí objektu SpinEdit, jehož hodnoty mohou být
pouze celočíselné. Váhu je třeba interpretovat jako procenta (jednička znamená stoprocentní váhu).
generuje body Bézierovy racionální
plochy. Váhy mají analogický význam jako v jednorozměrném případě. Jejich
velikost určuje vzdálenost plochy od příslušných řídících bodů. Jsou-li všechny
váhy rovny jedné, dostáváme „klasickou“ Bézierovu plochu. V řešeném příkladu
zadává uživatel váhové koeficienty pomocí objektu SpinEdit, jehož hodnoty mohou být
pouze celočíselné. Váhu je třeba interpretovat jako procenta (jednička znamená stoprocentní váhu).
Zde najdete kompletní zdrojový kód
a
zde spustitelný kód
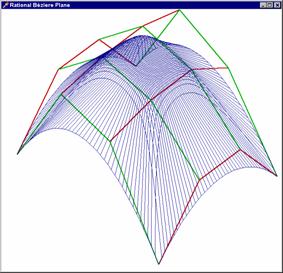

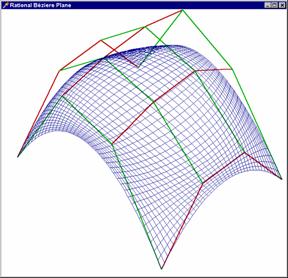

Na připojených obrázcích si
můžete prohlédnout, jak tato plocha vypadá pro váhy ![]() a pro čtyři
„prostřední“ váhy je v prvním případě
a pro čtyři
„prostřední“ váhy je v prvním případě ![]() , ve druhém pak
, ve druhém pak ![]() .
.
Fergusonovy
plochy
Tyto plochy vznikly v r. 1964 pro potřeby firmy Boeing a jsou dvojrozměrným zobecněním Fergusonových křivek (viz kpt. 3.8). Jsou určeny rovnicí
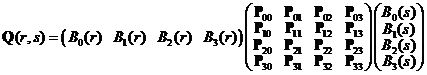
kde ![]() ;
; ![]() ;
;
![]() jsou body určující
rohy plochy,
jsou body určující
rohy plochy, ![]() tečné
vektory v rozích a
tečné
vektory v rozích a ![]() třísložkové zkruty v rozích. Při
zadávání musíme mít na paměti orientaci tečných vektorů a zkrutů dle
schématu:
třísložkové zkruty v rozích. Při
zadávání musíme mít na paměti orientaci tečných vektorů a zkrutů dle
schématu:
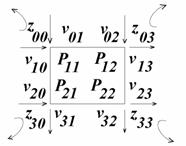
Pokud označíme všechny prvky
matice písmenem ![]() , je Fergusonova plocha určena rovnicí
, je Fergusonova plocha určena rovnicí
![]()
a její implementace je téměř
shodná s Bézierovou bikubickou plochou (liší se pouze polynomy ![]() místo
místo ![]() ). Jsou-li zkruty
). Jsou-li zkruty ![]() nulové vektory, jedná
se o plochu dvanáctivektorovou, neboť je určena dvanácti prvky (čtyřmi
rohy a osmi tečnými vektory), jinak mluvíme o ploše
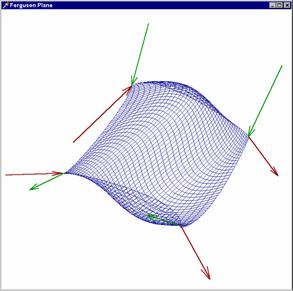
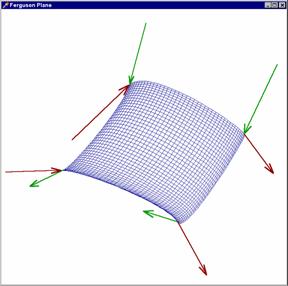
šestnáctivektorové (přibývají čtyři zkruty). Na těchto obrázcích vidíte plochu
dvanáctivektorovou a plochu šestnáctivektorovou s týmiž tečnými
vektory.
nulové vektory, jedná
se o plochu dvanáctivektorovou, neboť je určena dvanácti prvky (čtyřmi
rohy a osmi tečnými vektory), jinak mluvíme o ploše
šestnáctivektorové (přibývají čtyři zkruty). Na těchto obrázcích vidíte plochu
dvanáctivektorovou a plochu šestnáctivektorovou s týmiž tečnými
vektory.
Zde najdete kompletní zdrojový kód
a
zde
spustitelný
kód
Coonsovy plochy
Coonsova plocha
řízená polygonem: je opět
zobecněním Coonsovy kubiky. Situace je velmi podobná předchozímu případu
a z programátorského hlediska se liší pouze tvarem použitých
polynomů. Rovnici této
plochy můžeme psát ve tvaru:
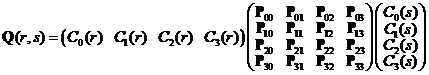
kde polynomy ![]() jsou tentokrát tvaru
jsou tentokrát tvaru
![]()
![]()
Příklad 1: Naprogramujme Coonsovu plochu řízenou
polygonem. Polynomy ![]() nastavíme ve Function C analogicky jako v předchozím příkladě
a zbytek kódu můžeme převzít zcela beze zbytku.
nastavíme ve Function C analogicky jako v předchozím příkladě
a zbytek kódu můžeme převzít zcela beze zbytku.
Výstup vidíme na připojeném obrázku.
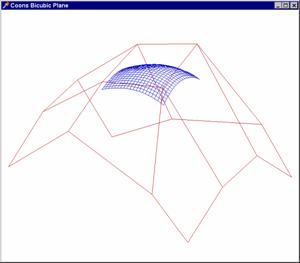
Zde najdete kompletní zdrojový kód a
zde spustitelný kód
Řídící polygon již není tak názorný jako u plochy Bézierovy, Coonsovy
plochy však patří v technické praxi k nejpoužívanějším. Jejich hlavní
výhoda je totiž v jejich napojování. Vhodnou volbou řídících polygonů
jednotlivých plátů lze totiž docílit toho, že výsledná plocha má hladkost
druhého stupně (plocha má spojité i druhé parciální derivace) a je
tedy hladší než plocha plátovaná z Bézierových ploch. Spojení Coonsových
plátů této hladkosti dosáhneme prostou duplikací tří řad „starého“ řídícího polygonu. Nový polygon se tedy od starého liší jen v jedné
řadě.
Příklad 2.: Napojování Coonsových
plátů řízených polygonem: Programování tohoto napojování je velmi jednoduché.
Jako příklad uvádíme napojování podél hran polygonu indexovaných indexem j
(čtyřčlenný polygon se třikrát opakuje pomocí indexu i): for i:=0 to 2
do for
j:=0 to 3 do P[i,j]:=P[i+1,j]; čtvrtý pak
dodefinujeme takto: for j:=0 to 3 do P[3,j]:=......; Zbytek
kódu je zcela analogický příkladu 16. Výstup je opět přiložen (je vynecháno
nyní již zcela nenázorné vykreslení řídících polygonů).
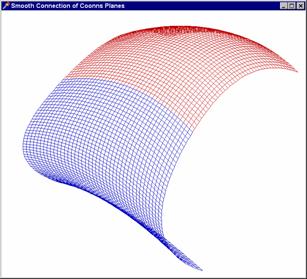
Zde najdete kompletní zdrojový kód
a
zde spustitelný kód
Coonsova plocha definovaná okrajem: je jednoznačně určena čtyřmi křivkami,
které musí tvořit její uzavřenou hranici. Určeme plochu parametrickými rovnicemi
s parametry ![]() jinými slovy pomocí parametrů
jinými slovy pomocí parametrů ![]() určeme
libovolný bod plochy
určeme
libovolný bod plochy ![]() . Bez újmy
na obecnosti můžeme předpokládat, že
. Bez újmy
na obecnosti můžeme předpokládat, že ![]() , neboť
každou plochu či křivku lze parametrizovat tak, aby tato podmínka byla splněna.
Je-li tedy plocha dána (zatím neznámým) předpisem
, neboť
každou plochu či křivku lze parametrizovat tak, aby tato podmínka byla splněna.
Je-li tedy plocha dána (zatím neznámým) předpisem ![]() ;
; ![]() , pak pro jednotlivé okrajové křivky jsou zřejmě
splněny podmínky:
, pak pro jednotlivé okrajové křivky jsou zřejmě
splněny podmínky:
1. křivka: ![]() ; 2. křivka:
; 2. křivka: ![]() ;
;
3. křivka: ![]() ; 4. křivka:
; 4. křivka:
![]() ;
;
Označme tedy předpisy pro známé
hraniční křivky symbolicky ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Neznámý předpis pro plochu je
. Neznámý předpis pro plochu je ![]() , rohy plochy tvoří body
, rohy plochy tvoří body ![]() ;
; ![]() ;
; ![]() ;
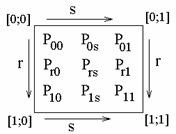
; ![]() .. Na připojeném schématu vidíte
popsaný půdorys této plochy, ze kterého je také patrná matice použitá při jejím
analytickém vyjádření. Tato plocha má totiž rovnici
.. Na připojeném schématu vidíte
popsaný půdorys této plochy, ze kterého je také patrná matice použitá při jejím
analytickém vyjádření. Tato plocha má totiž rovnici
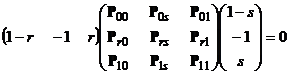
Toto implicitní vyjádření je sice
velmi názorné, pro algoritmizaci však nevhodné. Pro implementaci na počítači je
třeba matice na levé straně roznásobit a jedinou neznámou ![]() je třeba vyjádřit. To
přenechávám čtenáři jako cvičení a uvádím pouze výsledek:
je třeba vyjádřit. To
přenechávám čtenáři jako cvičení a uvádím pouze výsledek:
![]() (1)
(1)
Dostáváme tak explicitní parametrické vyjádření plochy vhodné pri implementaci na počítači, které je třeba již jen třikrát rozepsat do jednotlivých souřadnic.
Příklad 3.: Sestrojme algoritmus pro znázornění plochy určené okrajem.
procedure TDraw3D.CoonsPlane(Sender: TObject);
var Prs :TArrayOf3DPoints;
{pole
bodů pro vykreslování povrchových křivek}
Alfa,Beta:Double; {pohledové úhly}
i,j :Integer;
{indexy}
Pr0,Pr1,P0s,P1s,P00, P01,P10,P11:T3DPoint; {body matice plochy}
Procedure Border1(t:Real;var
P:T3DPoint); {parametrické
rovnice první okrajové křivky}
begin
P[1]:=0; P[2]:=t; P[3]:=cos(1)/Sin(1)*Sin(2*(0.5-t))/
Procedure
Border2(t:Real;var P:T3DPoint);
{parametrické
rovnice druhé okrajové křivky}
.........................................
Procedure Border3(t:Real;var
P:T3DPoint);
{parametrické
rovnice třetí okrajové křivky}
.........................................
Procedure Border4(t:Real;var
P:T3DPoint);
{parametrické
rovnice čtvrté okrajové křivky}
.........................................
begin
With Draw3D do
{uživatelská soustava
a pohledové úhly}
begin
x1:=-0.7;x2:=0.8;y1:=-1.5;y2:=1;
Scale(x1,x2,y1,y2);Alfa:=40;Beta:=20;View(Alfa,Beta);
end;
P00[1]:= 0;P00[2]:= 0;P00[3]:= 1; P10[1]:= 1;P10[2]:= 0;P10[3]:=-1; {rohy plochy}
P11[1]:= 1;P11[2]:= 1;P11[3]:=-1; P01[1]:=
0;P01[2]:= 1;P01[3]:=-1;
hr:=0.05;i:=1;r:=0;
{první okraj}
While r<=1+hr do
begin Border1(r,Prs[i]);i:=succ(i);r:=r+hr;
end;
PolyLine(Prs,i-1,200,0,200);
.............................................. {další okraje analogicky}
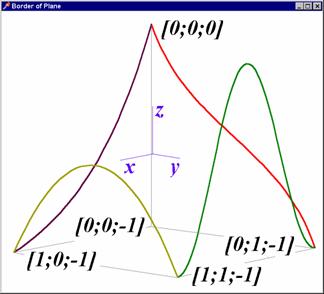
Okraje plochy (viz procedury Border1 - Border4) jsou rovinné (tedy jednoparametrické) křivky, které musí být navrženy tak, aby na sebe v prostoru navazovaly. Jejich prostorové rozmístění nad stranami čtverce bude dáno tím, že budou „přičítány správným směrem“ k rohům plochy. Parametrickými rovnicemi v Border1-Border4 je třeba zajistit správné „rozpětí“ a výšku jejich koncových bodů.
r:=0;hr:=0.05;hs:=0.05;
{konstrukce plochy
- první osnova řezů}
While r<1+hr do
begin
s:=0;i:=1;
While s<1+hs do
begin
Border1(s,P0s);Border2(r,Pr1);
Border3(s,P1s);Border4(r,Pr0);
{první souřadnice
i tého bodu pole - viz rovnice (1) }
Prs[i,1]:=-P00[1]*(1-r)*(1-s)+Pr0[1]*(1-s)-P10[1]*r*(1-s)
+P0s[1]*(1-r)+P1s[1]*r-P01[1]*(1-r)*s+Pr1[1]*s-P11[1]*r*s;
Prs[i,2]:=-P00[2]*(1-r)*(1-s)+Pr0[2]*(1-s)-P10[2]*r*(1-s)+…
{druhá souřadnice i tého bodu pole-viz rovnice (1)}
Prs[i,3]:=-P00[3]*(1-r)*(1-s)+......;
{třetí souřadnice i tého bodu pole-viz rovnice (1)}
s:=s+hs;i:=succ(i);
end;
PolyLine(Prs,i-1,200,0,0);r:=r+hr;
end;
……………………. {druhá osnova řezů přehozením cyklů}
end;
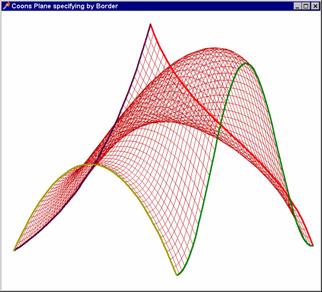
Zde najdete kompletní zdrojový kód
a zde spustitelný kód
Jestliže dvě protilehlé okrajové křivky budou přímky, dostáváme speciální případ plochy určenou okrajem, tzv. plochu přímkovou (v tom případě je celá jedna soustava řezů tvořena přímkami).
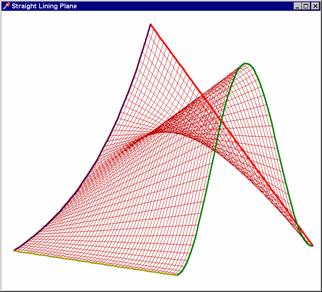
Obecně nemusí mít bilineární plochy čtvercový půdorys (ztotožněním dvou rohů plochy lze např. obdržet i zde trojúhelníkové pláty), hraniční křivky dokonce nemusí být ani rovinné. Konstrukce těchto ploch je však poněkud obtížnější a vymyká se rozsahu tohoto textu.