Realistické zobrazování prostorových objektů
K tomu, aby objekt
znázorňovaný na obrazovce počítače působil
realisticky, je třeba vyřešit několik problémů. První již vyřešen máme:
a) volba vhodného promítání na výstupní
zařízení. Pro tyto účely je zcela nevhodná kosoúhlá
axonometrie. Není vhodné ani promítání na
kulovou a válcovou plochu (to známe z uměleckých fotografií
pořízených objektivy s velmi širokým zorným úhlem). Nejjednodušším
vhodným promítáním je kolmá axonometrie. Hodí se ke
zobrazování objektů, které pozorujeme ve velmi malých zorných úhlech.
Tyto objekty musí být tedy buď velmi malé, nebo velmi vzdálené od pozorovatele. Chceme-li nějakým
způsobem znázornit velikost objektu, je vhodnější lineární perspektiva. Její střed bychom však měli volit tak, abychom nepřekračovali zorný
úhel 40o, neboť bychom se zase ocitli spíše v oblastech
širokoúhlé fotografie.
b) viditelnost. Je třeba vymyslet algoritmus, který zobrazí jen viditelné části
objektu, tj. ty části, jejichž promítací
paprsek není na cestě k pozorovateli přerušen.
c) optické vlastnosti povrchu objektu. Vzhled povrchu reálného
předmětu závisí na řadě jeho fyzikálních vlastností:
na barvě povrchu, na procentu odraženého a pohlceného světla (tj. zda je
předmět lesklý či matný), na hladkosti povrchu, indexu lomu atd. Čím více těchto vlastností algoritmus postihuje, tím věrohodněji
bude objekt působit.
d) vržené stíny a odlesky. Jeden
zobrazovaný objekt má vliv na druhý. Vrhá stíny,
lesklý předmět odráží světlo, které může dopadnout na
jiný objekt nebo na podložku atd.
Vzhledem
k omezenému rozsahu textu se nelze zabývat všemi optickými jevy, všimneme
se jen těch nejdůležitějších.
Viditelnost
Základním
problémem při realistickém zobrazování prostorových útvarů je určit, které
části objektu jsou viditelné a které zakryté. Existuje spousta algoritmů, které tuto úlohu řeší. Jeden z nejrozšířenějších je tzv. malířův
algoritmus (Painter's algorithm, Priority list). Princip
spočívá v přímém vykreslování ploch na obrazovku,
a to v pořadí od nejvzdálenějších po nejbližší vzhledem
k pozorovateli. Bližší plochy překryjí vzdálenější
a viditelnost je tak vyřešena přirozeným způsobem. Při realizaci
tohoto algoritmu však narážíme na dva problémy:
1. Plochy se mohou překrývat dosti složitým způsobem. Někdy
nelze jednoznačně rozhodnout, která plocha má být kreslena dříve
a viditelnost je třeba řešit dosti složitými testy. Rozbor těchto situací přesahuje rámec tohoto textu a nebudeme
se jimi zabývat.
2. Aby později kreslená plocha překryla plochu dříve kreslenou, je třeba
každou plochu vyplnit určitou barvou.
Segmentace plochy z = f(x; y): protože se budeme nyní
zabývat plochami vyjádřenými analyticky, stojíme v první řadě před úkolem,
jak plochu rozdělit na jednotlivé části, jak ji
segmentovat. Předpokládejme spojitou funkci 
definovanou na obdélníku 
. Plochu budeme interpolovat rovinnými segmenty, a to tak, že na osách zvolíme dělení pomocí kroků 
, 
a těmito kroky
cyklujeme přes intervaly 
,
.
Vrcholy segmentu mají pak
souřadnice:
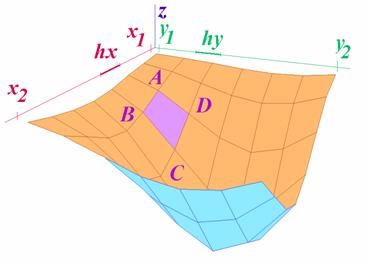
Segmenty nejsou
obecně rovinné, je proto třeba segment sestrojovat jako dva trojúhelníky, např. 
, 
.
Předpokládejme
nejdříve, že trojúhelník již máme promítnutý do roviny a jeho vrcholy převedeny
do světových souřadnic. Tyto body jsou tedy typu TPixel, který je
deklarován jako
Type TPixel = array [1..2]
of Integer:
Procedure
TDraw3D.FillTriangle2D(X,Y,Z:TPixel;Red,Green,Blue:Byte);
Const
TempRed=254;TempGreen=254;TempBlue=254;
{barevné složky prozatímní hranice}
Var i,j,h1,h2,Adr,
{indexy}
MinI,MaxI,MinJ,MaxJ:Integer; {vrcholy
opsaného obdélníka}
BorderLine :Boolean; {identifikátor hranice}
ScanRow :PByteArray; {řádek bitmapy}
begin
Line2D(X,Y,TempRed,TempGreen,TempBlue);
Line2D(Y,Z,TempRed,TempGreen,TempBlue);
Line2D(X,Z,TempRed,TempGreen,TempBlue); {ohraničení
segmentu}
Min1:=X[1];Max1:=X[1];
Min2:=X[2];Max2:=X[2];
if Y[1]<Min1 then Min1:=Y[1] else
if Y[1]>Max1 then Max1:=Y[1];
if Y[2]<Min2 then Min2:=Y[2]
else if Y[2]>Max2 then Max2:=Y[2];
if Z[1]<Min1 then Min1:=Z[1]
else if Z[1]>Max1 then
Max1:=Z[1];
if Z[2]<Min2 then Min2:=Z[2]
else if Z[2]>Max2 then
Max2:=Z[2];
For
j:=Min2 to Max2
do
begin
ScanRow:=Image.Picture.Bitmap.ScanLine[j];
i:=Pred(Min1);
Repeat
{postup k hranici segmentu zleva}
inc(i);Adr:=3*i;
BorderLine:=(ScanRow[Adr]=TempBlue)
and (ScanRow[succ(Adr)]=TempGreen) and
ScanRow[succ(succ(Adr))]=TempRed);
Until
(i=Max1) or BorderLine;
if BorderLine
then begin
h1:=i; i:=succ(Max1);
{nastavení
levého krajního bodu vyplňované úsečky}
Repeat
{postup k hranici segmentu zprava}
dec(i);Adr:=3*i;
BorderLine:=(ScanRow[Adr]=TempBlue)
and (ScanRow[succ(Adr)]=TempGreen) and
(ScanRow[succ(succ(Adr))]=TempRed)
Until
(i=h1) or BorderLine;
h2:=i;
{nastavení pravého krajního bodu}
For i:=h1 to h2 do
begin
{sestrojení úsečky}
Adr:=3*i;
ScanRow[Adr]:=Blue;
ScanRow[succ(Adr)]:=Green;
ScanRow[succ(succ(Adr))]:=Red;
end;
end;
end;
end;
Pomocí této
procedury pak sestrojíme trojúhelník v prostoru. Podle zvoleného typu
promítání promítneme vrcholy do průmětny (procedura Projection), průměty
převedeme do světových souřadnic a použijeme FillTriangle2D.
procedure
FillTriangle(A,B,C:T3DPoint;Red,Green,Blue :byte);
var
pX,pY,pZ :T2DPoint;
X,Y,Z :TPixel;
begin
Projection(A,pX);Projection(B,pY);Projection(C,pZ);
X[1]:=XCoor(pX[1]);X[2]:=YCoor(pX[2]);
Y[1]:=XCoor(pY[1]);Y[2]:=YCoor(pY[2]);
Z[1]:=XCoor(pZ[1]);Z[2]:=YCoor(pZ[2]);
FillTriangle2D(X,Y,Z,Red,Green,Blue);
end;
Pro případné rozlišení rubu
a líce plochy (pokud tyto strany budeme chtít sestrojovat různými barvami) si
připravíme následující procedury a funkce:
Procedure
SetVector(X,Y:T3DPoint;var v:TVector);
{nastavení vektoru z krajních bodů}
begin
v[1]:=Y[1]-X[1];v[2]:=Y[2]-X[2];v[3]:=Y[3]-X[3];
end;
Procedure
VectorProduct(r,s:TVector;var t:TVector);
{vektorový součin vektorů}
begin
t[1]:= r[2]*s[3]-s[2]*r[3]; t[2]:=-r[1]*s[3]+s[1]*r[3]; t[3]:=
r[1]*s[2]-s[1]*r[2];
end;
function
CosAngle(u,v:TVector):Double;
{kosinus úhlu dvou vektorů}
begin
CosAngle:=(u[1]*v[1]+u[2]*v[2]+u[3]*v[3])/Sqrt(u[1]*u[1]+u[2]*u[2]+u[3]*u[3])
/Sqrt(v[1]*v[1]+v[2]*v[2]+v[3]*v[3])
end;
Při konstrukci plochy zadané
rovnicí není třeba zjišťovat
vzdálenosti jednotlivých segmentů od pozorovatele,
stačí na obou osách postupovat vhodným směrem. V případě, že se
pozorovatel nachází
begin
hx:=(x2-x1)/CountOfSegments;hy:=(y2-y1)/CountOfSegments;
y:=y1;
Repeat
x:=x1;
Repeat
A[1]:=x; A[2]:=y; A[3]:=f(x,y);
B[1]:=x+hx;B[2]:=y; B[3]:=f(x+hx,y);
C[1]:=x+hx;C[2]:=y+hy;C[3]:=f(x+hx,y+hy);D[1]:=x;
D[2]:=y+hy;D[3]:=f(x,y+hy);
FillTriangle(A,B,C,Red,Green,Blue);
FillTriangle(C,D,A,Red,Green,Blue);
x:=x+hx;
until x>x2;
y:=y+hy;
until y>y2;
end;
Poznámky:
1. Procedura FillTriangle2D
používá při vyplňování přístup do obrazových řádků bitmapy, nikoli matici
Pixels objektu Canvas. Vyplňování se tak podstatně urychlí.
2. Výše uvedená sekvence
kódu nerozlišuje rub a líc plochy. Abychom dostali výstup analogický připojenému
obrázku, je třeba tyto strany rozlišit a každou z nich vyplňovat jinou barvou.
Červeně uvedené
procedury FillTriangle je pak třeba nahradit následující sekvencí:
SetVector(B,C,u);SetVector(B,A,v);
VectorProduct(u,v,w); {w je normála
segmentu ABC}
if CosAngle(w,MajorRay)>0
{je-li úhel normály
segmentu a směru pohledu kladný}
then
begin
{vyplňuj barvou pro
líc}
FillTriangle(A,B,C,RightRed,RightGreen,RightBlue);
Surf1:=Right;
end
else begin
{jinak vyplňuj barvou pro rub}
FillTriangle(A,B,C,WrongRed,WrongGreen,WrongBlue);
Surf1:=Wrong;
end;
SetVector(D,A,u);SetVector(D,C,v);
VectorProduct(u,v,w);
{totéž pro segment
CDA}
if
CosAngle(u,w)>0
then begin
FillTriangle(C,D,A,RightRed,RightGreen,RightBlue);
Surf2:=Right;
end
else begin
FillTriangle(C,D,A,WrongRed,WrongGreen,WrongBlue);
Surf2:=Wrong;
end;
Line(A,B,0,0,0);Line(B,C,0,0,0);
Line(C,D,0,0,0);Line(D,A,0,0,0); {obvod segmentu ABCD}
if
Surf1<>Surf2
then Line(A,C,0,0,0); {jsou-li
trojúhelníky vidět z různých stran, sestroj i AC}
Příklad 1.: Řeší sestrojení
plochy pomocí výše uvedených
algoritmů. Na obrázku výše je
výstup pro funkci definované
na obdélníku
.
Zde najdete kompletní zdrojový kód a zde spustitelný kód
Je-li plocha zadaná
parametrickými rovnicemi 
kde 
, je
situace při konstrukci segmentů je zcela analogická. Pomocí kroků 
resp. 
zvolíme
dělení intervalů a těmito kroky opět cyklujeme přes intervaly 
; 
. Vrcholy jednotlivých segmentů mají tentokrát
souřadnice:
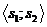
Můžeme beze změny použít
výše popsanou proceduru DrawSegment, nelze však „ošidit“ určování pořadí
konstrukce segmentů podle vzdálenosti od pozorovatele tak, jak se nám to
poštěstilo v předchozím případě. Chceme-li zajistit konstrukci segmentů
plochy v pořadí daném jejich vzdáleností od
pozorovatele, můžeme postupovat vpodstatě dvojím způsobem:
a) Algoritmus, který bychom mohli označit jako „postup ve vrstvách“. Spočívá v tom, že se k pozorovateli blížíme
v tenkých vrstvách a v každé vrstvě jsou vykresleny pouze
segmenty, které v ní leží. Pro vykreslení či nevykreslení segmentu
bude rozhodující vzdálenost jednoho z jeho vrcholů od
roviny kolmé ke směru pohledu. Nejjednodušší je volit rovinu
procházející počátkem. Je-li její normálový vektor 
, pak vzdálenost bodu 
od této
roviny je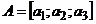 
. Je-li vektor v jednotkový, je jmenovatel tohoto zlomku roven jedné, vynecháme-li
navíc absolutní hodnotu, pak znaménko této „vzdálenosti“ navíc říká, zda bod 
je před nebo za touto rovinou vzhledem
k pozorovateli.
begin
hr:=(r2-r1)/CountOfSegments;
hs:=(s2-s1)/CountOfSegments;
Min:=1e6;Max:=-1e6;
r:=r1;
Repeat {určení minimální
a maximální potřebné vzdálenosti od pozorovatele}
s:=s1;
Repeat
A[1]:=Fi(r,s);A[2]:=Psi(r,s);A[3]:=Tau(r,s);
Distance:=Draw3D.MajorRay[1]*A[1]+Draw3D.MajorRay[2]*A[2]
+Draw3D.MajorRay[3]*A[3];
if Min>Distance then Min:=Distance
else if Max<Distance then
Max:=Distance;
s:=s+hs;
until
s>s2;
r:=r+hr;
Until
r>r2;
Layer:=Min;
{Nastavení zadní
krajní polohy}
While
Layer<Max do
{Dokud neprojdeš
celý pás}
begin
r:=r1;
Repeat
{projdi celou
plochu}
s:=s1;
Repeat
A[1]:=Fi(r,s);A[2]:=Psi(r,s);A[3]:=Tau(r,s);
{vypočítej vrchol A segmentu a jeho vzdálenost od roviny}
Distance:=MajorRay[1]*A[1]+MajorRay[2]*A[2]
+MajorRay[3]*A[3]-Layer;
if abs(Distance)<2*hr {je-li rozdíl vzdálenosti roviny a procházené}
then begin
{vrstvy menší než daná hodnota}
s:=s+hs;B[1]:=Fi(r,s);A[2]:=Psi(r,s);
A[3]:=Tau(r,s);
{vypočítej ostatní vrcholy}
r:=r+hr;C[1]:=Fi(r,s);
C[2]:=Psi(r,s);C[3]:=Tau(r,s);
s:=s-hs;D[1]:=Fi(r,s);
D[2]:=Psi(r,s);D[3]:=Tau(r,s);
r:=r-hr;
{a segment
nakresli}
FillTriangle(A,B,C,Red,Green,Blue);
FillTriangle(C,D,A,Red,Green,Blue);
end;
s:=s+hs;
until s>s2;
r:=r+hr;
until r>r2;
Layer:=Layer+2*hr;
end;
end;
(červeně
vyznačené procedury lze případně opět doplnit dle předchozího příkladu)
Příklad 2.: Zobrazte anuloid
s viditelností ve středovém promítání. Příklad
je řešen s použitím výše uvedených algoritmů. Vzhledem
k tomu, že parametrické rovnice zadává uživatel jako řetězce, je
k výpočtu hodnot vrcholů jednotlivých segmentů použita opět funkce Calc (popř.
funkce PreCAlc
a PostCalc).
Jména vstupních řetězců jsou pořadě fa, fb, fc, místo např.
C[2]:=Psi(r,s) je třeba psát C[2]:=Calc(fb,ErrorReport).
Na připojeném obrázku je výstup pro .
Zde najdete kompletní zdrojový kód
a zde spustitelný kód
b) Spočítáme všechny segmenty plochy a uspořádáme
je podle vzdálenosti. Tento algoritmus je náročnější na
paměť a jeho rychlost závisí na efektivnosti použitého třídícího algoritmu.
Celou plochu budeme deklarovat jako pole segmentů, což bude záznam čtyř vrcholů
a vzdálenosti od pozorovatele:
Type TSegment = record A,B,C,D :T3DPoint;
Dist :Double;
end;
var
Segment :array [0..50000] of TSegment;
Pro uspořádání pole segmentů
podle jejich vzdálenosti od pozorovatele použijeme lze
použít např. tzv. bublinovou
metodu, která je ovšem pro tyto účely dosti pomalá. Použijeme proto podstatně
efektivnější rekurzivní proceduru:
procedure
sort(Left,Right:LongInt);
var
i,j :LongInt;
Pivot :Double;
Trezor :TSegment;
begin
i:=Left;j:=Right;
pivot:=Segment[(Left+Right)
div 2].Dist;
repeat
while Segment[i].Dist<pivot do inc(i);
while Segment[j].Dist>pivot do dec(j);
if i<=j then
begin
Trezor:=Segment[i];Segment[i]:=Segment[j];
Segment[j]:=Trezor;inc(i);dec(j);
end;
until i>j;
if Left<j then
sort(Left,j);
if Right>i then
sort(i,Right);
end;
Ve vlastní vykreslovací
proceduře nejdříve naplníme pole segmentů:
r:=r1;n:=0;
Repeat
s:=s1;
Repeat
With
Segment[n] do
begin
A[1]:=Fi(r,s);A[2]:=Psi(r,s);A[3]:=Tau(r,s);
B[1]:=Fi(r+hr,s);B[2]:=Psi(r+hr,s);B[3]:=Tau(r+hr,s);
C[1]:=Fi(r+hr,s+hs);C[2]:=Psi(r+hr,s+hs);
C[3]:=Tau(r+hr,s+hs);
D[1]:=Fi(r,s+hs);D[2]:=Psi(r,s+hs);
D[3]:=Tau(r,s+hs);
Dist:=sqr(ObserverPoint[1]-A[1])
+sqr(ObserverPoint[2]-A[2])+sqr(ObserverPoint[3]-A[3]);
end;
inc(n);
s:=s+hs;
until s>s2;
r:=r+hr;
until r>r2;
dec(n);Sort(0,n); {třídění}
For
i:=n downto
0 do {vykreslení}
With
Segment[n] do
begin
FillTriangle(A,B,C,Red,Green,Blue);
FillTriangle(C,D,A,Red,Green,Blue);
End;
(opět
s možností modifikace vyplňovacích příkazů)
Příklad 3.: využívá výše uvedeného
algoritmu.
Zde najdete kompletní zdrojový kód
a zde
spustitelný kód
Tento algoritmus je
většinou rychlejší, než algoritmus vrstvový, o čemž se můžeme přesvědčit v
následujícím příkladě.
Příklad 4.:
umožňuje porovnání rychlostí dvou výše uvedených algoritmů.
Zde najdete kompletní zdrojový kód
a zde
spustitelný kód
Příklad 5.: Zobrazte krychli
s viditelností v kolmé axonometrii. Dosud jsme
znázorňovali jednobarevné plochy. Tento příklad ukazuje,
že u každého segmentu můžeme navíc definovat i jeho vlastní barvu.
Toho využijeme především později při nanášení textur.
Algoritmus sestrojí tři „pevné“ stěny
krychle a řez
kolmý na některou ze souřadných os. Souřadnou osu
a bod, kterým řez prochází definuje uživatel. Tento
algoritmus sestrojuje krychli tak, že každá její stěna se skládá z
jednobarevných
čtvercových segmentů. Na připojeném obrázku je řez
kolmý na osu 
, který ji protíná v bodě 
. Viditelnost řešena prostým
pořadím konstrukce.
Zde najdete kompletní zdrojový kód a zde spustitelný kód
Tuto úlohu je však možno
řešit také podstatně efektivněji, a to tzv. interpolací barvy. Základem algoritmu je interpolace barvy na úsečce v rovině. Zde již nemůžeme
použít objekt Canvas, neboť ten interpolovat barvu neumí. Úlohu musíme řešit ve vlastní režii vlastní procedurou - nazvěme ji
InterpolLine2D. Jejími parametry jsou krajní pixely a
jejich barvy. Souřadnice bodů ležících na
úsečce počítáme stejně, jako u jednobarevné úsečky (viz matematické podrobnosti
2. kapitoly). Výpočet barvy ukažme na části kódu
sestrojující úsečku s kladnou směrnicí menší než jedna:
procedure
TDraw3D.InterpolLine2D
(X,Y:TPixel;RedX,GreenX,BlueX,
RedY,GreenY,BlueY:Byte);
var
p,p1,p2,Dx,Dy,i :Integer;
{přírůstky a index}
M :TPixel;
{bod probíhající
úsečku}
R,G,B,StepR,StepG,StepB:Single; {aktuální bar. složky a jejich přírůstky}
ScanRow :PByteArray; {pole
ukazatelů na obrazový řádek}
Adr :Integer; {pozice na obrazovém řádku}
Begin
Dx:=Y[1]-X[1];
Dy:=Y[2]-X[2];
{přírůstky na osách}
M[1]:=X[1];M[2]:=X[2];
{počáteční bod a jeho konstrukce}
ScanRow:=Image.Picture.Bitmap.ScanLine[M[2]];
Adr:=3*M[1];
ScanRow[Adr]:=BlueX;
ScanRow[succ(Adr)]:=GreenX;
ScanRow[succ(succ(Adr))]:=RedX;
if (Dx>0)
and (Dy>0) and (Dx>Dy)
{vybraná poloha 0<k<1}
then begin
StepR:=(RedY-RedX)/DX;
{nastavení barevných kroků}
StepG:=(GreenY-GreenX)/DX;
StepB:=(BlueY-BlueX)/DX;
R:=RedX;G:=GreenX;B:=BlueX;
{počáteční barva}
p1:=2*Dy;p2:=2*(Dy-Dx);p:=2*Dy-Dx;
{nastavení prediktorů}
ScanRow:=Image.Picture.Bitmap.ScanLine[M[2]];
While
M[1]<Y[1] do
{postup po
úsečce}
begin
inc(M[1]);
{skok na
následující x-ovou souřadnici}
if p>0 then begin {výpočet a nastavení y-ové souřadnice}
inc(M[2]);p:=p+p2;
ScanRow:=
Image.Picture.Bitmap.ScanLine[M[2]];
end
else p:=p+p1;
Adr:=3*M[1];
R:=R+StepR;G:=G+StepG;B:=B+StepB; {skok na následující barvu}
ScanRow[Adr]:=Round(B);
{obarvení bodu}
ScanRow[succ(Adr)]:=Round(G);
ScanRow[succ(succ(Adr))]:=Round(R);
end;
end;
Pomocí takto
barevně interpolované úsečky můžeme sestrojit barevně interpolovaný
trojúhelník. Postup je analogický jako v proceduře FillTriangle s těmito rozdíly:
Konstrukce popsané v této proceduře, tj. ohraničení
trojúhelníka „prozatímní“ barvou za účelem rozpoznání hranic pro vyplnění a
nalezení hranice na jednotlivých obrazových řádcích (proměnné h1, h2) je třeba
provádět do pomocného („paměťového“) obrazu (v
řešeném příkladu i na připojeném obrázku je označen jako MemoryImage. Hranice
sestrojovaného trojúhelníku je totiž konstruována výše uvedenou procedurou
InterpolLine2D, nemá konstantní barvu a nebylo by ji tak možno rozeznat.
Vodorovné úsečky ohraničené proměnnými h1, h2 jsou rovněž
prováděny interpolovanou úsečkou. Takto rastrově vyplňovaný průmět trojúhel-níku
je základem procedury
FillInterpolTriangle(A,B,C, RedA,GreenA,BlueA, RedB,GreenB,BlueB,
RedC,GreenC,BlueC)
s jejíž pomocí
snadno sestrojujeme barevně interpolované stěny. Např.
řez krychlí rovnoběžný se
stěnou
a na ose Green
procházející bodem
vypadá takto:
A[1]:=255;A[2]:=150;A[3]:=255; B[1]:=255;B[2]:=150;B[3]:= 0;
C[1]:=
0;C[2]:=150;C[3]:= 0;
D[1]:= 0;D[2]:=150;D[3]:=255;
FillInterpolTriangle(A,B,C,
Trunc(A[1]),Trunc(A[2]),Trunc(A[3]),
Trunc(B[1]),Trunc(B[2]),Trunc(B[3]),
Trunc(C[1]),Trunc(C[2]),Trunc(C[3]));
FillInterpolTriangle(C,D,A,
Trunc(C[1]),Trunc(C[2]),Trunc(C[3]),
Trunc(A[1]),Trunc(A[2]),Trunc(A[3]),
Trunc(D[1]),Trunc(D[2]),Trunc(D[3]));
Zde najdete kompletní zdrojový kód
a zde
spustitelný
kód
Plochy určené rovnicí 
Jak již bylo řečeno,
algoritmus konstrukce těchto ploch je trojrozměrným zobecněním algoritmu
konstrukce křivek 
(viz kpt.
3.4. odstavec Síťová konstrukce) . Zatímco rovinná křivka byla podmnožinou obdélníka 
, který jsme rozdělili rovinnou sítí na množinu obdélníků -
fyzických pixelů (
domén), plocha 
je podmnožinou kvádru 
, který rozdělíme prostorovou mřížkou na množinu kvádrů -
fyzických voxelů (
domén).
Ve dvojrozměrném případě jsme
pracovní plochu rozdělili na obdélníky , kde
; 
; 
; 
a zjišťovali jsme, zda křivka protíná testovaný
obdélník. To se stane zřejmě právě tehdy, když alespoň ve
dvou jeho vrcholech má funkce 
různá znaménka.
V trojrozměrném případě máme
pracovní objem rozdělen na kvádry 
, kde
; 
; 
; 
; 
; 
; 
.
Podobně jako ve
dvojrozměrném případě ohodnoťme i zde vrcholy kvádru postupně hodnotami 
; 
; 
;...;
, a to právě tehdy, když v příslušném vrcholu je 
, jinak vrcholu přiřaďme nulu. Celý kvádr tak může být
ohodnocen hodnotami 
. Z hlediska naší konstrukce je tedy celkem
256 možností, jak může plocha kvádr protínat. Kvádr na obrázku vlevo je
ohodnocen číslem 
, kvádr vpravo pak číslem 
. Součet těchto ohodnocení je 255 a je zřejmé, že postup
konstrukce bude v obou případech stejný - v obou případech je třeba hledat
průsečíky na hranách 
, 
, 
, 
, 
a nalezený řez pak
interpolovat celkem třemi trojúhelníky. Ačkoli je tedy celkový počet případů,
které je třeba řešit, dvě stě padesát čtyři (kvádry s ohodnoceními 0 resp.255
plocha neprotíná), program stačí větvit „pouze“ na sto dvacet sedm větví. Hodnoty řezů je opět možno názorně vyjádřit ve dvojkové soustavě,
popř. se pokusit o redukci větvení programu
pomocí symetrií jednotlivých případů. Je-li např. ohodnocení vyjádřeno jako mocnina dvou (tj. 
), znamená to, že platí právě v jenom
vrcholu a řezem je tedy jediný trojúhelník.
Vzhledem k tomu, co bylo
řečeno výše, dostáváme trojúhelníkový řez rovněž pro 
. Všech těchto šestnáct případů bychom tak
mohli řešit jedinou větví programu. Redukce počtu případů je ovšem možná
pouze dalším ne zrovna jednoduchým programováním rozpoznávání symetrií a jejich
převodem na jediný případ. Je tedy
otázkou, zda by výsledný program byl jednodušší. V
každém případě by však byl právě o toto rozpoznávání a tyto převody pomalejší.
V konkrétní programové
realizaci jsou hodnoty funkce ukládány do
trojrozměrného pole Grid. Průsečík plochy s testovanou
hranou bychom mohli opět hledat půlením intervalu tak, jako jsme to prováděli v
kpt. 3.4. (viz proceduru
HorizHalf resp. VertikHalf). Zde bychom museli rozlišovat
trojí půlení (ve směrech souřadných os). Poněkud
jednodušší a rychlejší postup je nalezení přibližného průsečíku lineární
interpolací. Tato interpolace zpracovává body X, Y, kde první tři
souřadnice udávají pozici bodu v mřížce (poli Grid), čtvrtá pak funkční hodnotu
funkce
. Procedura nastavuje souřadnice interpolovaného průsečíku
hrany XY s plochou :
Procedure Interpolation(X,Y:T3DPoint;var Z:T3DPoint);
begin
t:= - X[4]/(Y[4]-X[4]);
Z[1]:=X[1]+t*(Y[1]-X[1]);
Z[2]:=X[2]+t*(Y[2]-X[2]);
Z[3]:=X[3]+t*(Y[3]-X[3]);
end;
Do control panelu je
třeba kromě obvyklých parametrů zadat i pracovní objem pomocí proměnných
DefX1,...,DefZ2 a dále počet uzlových bodů na jeho nejdelší hraně. Všechny parametry
nutné pro chod programu pak přečte procedura Setting:
Procedure
TControl_Panel.Setting(Sender:TObject);
var Code:Integer;
begin
Val(EditDefX1.Text,DefX1,Code);
Val(EditDefX2.Text,DefX2,Code);:=Number;
Val(EditDefY1.Text,DefY1,Code);
Val(EditDefY2.Text,DefY2,Code);:=Number;
Val(EditDefZ1.Text,DefZ1,Code);
Val(EditDefZ2.Text,DefZ2,Code);:=Number;
Val(EditNodalPoints.Text,NoOfNodalPoints,Code);
end;
Vlastní procedura pak vypadá
následovně (uvádíme jen fragment):
begin
With
Draw3D do
begin
........................ {po
obvyklém načtení parametrů a nastavení měřítka}
Max:=DefX2-DefX1;
{zjistíme
nejdelší hranu pracovního objemu}
if DefY2-DefY1>Max then
Max:=DefY2-DefY1;
if DefZ2-DefZ1>Max then
Max:=DefZ2-DefZ1;
hx:=Max/(NoOfNodalPoints-1); {a nastavíme kroky vjednotlivých směrech}
hy:=hx;hz:=hx;
z:=DefZ1;k:=0;
{napočítáme funkční hodnoty v mřížce}
Repeat
x:=DefX1;i:=0;
Repeat
y:=DefY1;j:=0;
Repeat
Grid[k,i,j]:=f(x,y,z);y+hy;inc(j);
Until
y>DefY2;
x:=x+hx;inc(i);
Until
x>DefX2;
z:=z+hz;inc(k);
Until
z>DefZ2;
MaxI:=i-2;MaxJ:=j-2; MaxK:=k-2;
PocetSegmentu:=0;
{počet segmentů,
které je třeba sestrojit}
For
k:=0 to
MaxK do
For
j:=0 to
MaxJ do
For
i:=0 to
MaxI do
begin
{napočítáme vrcholy testovaného kvádru}
A[1]:= i;A[2]:=j;A[3]:=k;A[4]:=Grid[k,i,j];
B[1]:=succ(i);B[2]:=j;B[3]:=k;B[4]:=Grid[k,succ(i),j];
C[1]:=succ(i);C[2]:=succ(j);C[3]:=k;C[4]:=Grid[k,succ(i),succ(j)];
D[1]:=i;D[2]:=succ(j);D[3]:=k;D[4]:=Grid[k,i,succ(j)];
Ac[1]:=i;Ac[2]:=j;Ac[3]:=succ(k); Ac[4]:=Grid[succ(k),i,j];
Bc[1]:=succ(i);Bc[2]:=j;Bc[3]:=succ(k);Bc[4]:=Grid[succ(k),succ(i),j];
Cc[1]:=succ(i);Cc[2]:=succ(j);Cc[3]:=succ(k);Cc[4]:=Grid[succ(k),succ(i),succ(j)];
Dc[1]:=i;Dc[2]:=succ(j);Dc[3]:=succ(k); Dc[4]:=Grid[succ(k),i,succ(j)];
Citac:=0; {pomocí
této proměnné zjistíme „hodnotu“ testovaného kvádru}
if A[4]>0
then Citac:=Citac+1;
if
B[4]>0 then Citac:=Citac+2;
if C[4]>0 then
Citac:=Citac+4;
if
D[4]>0 then Citac:=Citac+8;
if Ac[4] >0 then
Citac:=Citac+16;
if
Bc[4]>0 then Citac:=Citac+32;
if Cc[4]>0 then
Citac:=Citac+64;
if Dc[4]>0 then
Citac:=Citac+128;
Case
Citac of
1,254:begin {znaménko funkce
se liší pouze v bodě A}
inc(PocetSegmentu); {je třeba nastavit jeden trojúhelníkový segment}
With
Segment[PocetSegmentu] do
begin {Vrcholy segmentu nastavíme jako průsečíky
na hranách AB, AD, AA'}
Interpolation(A,B,SegmA);
Interpolation(A,D,SegmB);
Interpolation(A,Ac,SegmC);
end;
end;
.......................................
59 ,196:begin {případy dle výše uvedených obrázků}
inc(PocetSegmentu); {je třeba nastavit tři trojúhelníkové segmenty}
With
Segment[PocetSegmentu] do
begin
Interpolation(Ac,Dc,SegmA);
Interpolation(D,Dc,SegmB);
Interpolation(Bc,Cc,SegmC);
end;
inc(PocetSegmentu);
With
Segment[PocetSegmentu] do
begin
Interpolation(C,D,SegmA);
Interpolation(D,Dc,SegmB);
Interpolation(Bc,Cc,SegmC);
end;
inc(PocetSegmentu);
With
Segment[PocetSegmentu] do
begin
Interpolation(C,D,SegmA);
Interpolation(B,C,SegmB);
Interpolation(Bc,Cc,SegmC);
end;
end;
.......................................
end;
{ Case Citac of}
Podobně jako v
př. 3. předchozí kapitoly následuje třídění
segmentů podle jejich vzdálenosti od pozorovatele algoritmem Quick Sort a
jejich vykreslení.
Příklad 1: Řeší konstrukci ploch výše uvedeným
algoritmem. Na připojeném obrázku si můžeme prohlédnout plochu pro
Zde najdete
kompletní zdrojový kód a zde spustitelný kód
Vlastní stín
Dalším krokem ke
zlepšení vzhledu zobrazovaného objektu je stínování. Reálné předměty jsou vyrobeny z různého materiálu
a jejich povrchy mají různý vzhled. Hovoříme-li
o vzhledu povrchu, říkáme, že je červený, lesklý, drsný, průhledný atd.
Tyto vlastnosti se vztahují vesměs k optickým
vlastnostem povrchu, popř. celého tělesa.
Dopadne-li světlo na povrch tělesa, je částečně
pohlceno a částečně odraženo. Předpokládejme
nejjednodušší případ, kdy je těleso přímo osvětleno jedním plošným zdrojem
bílého světla. Dopadá-li navíc světelný paprsek kolmo na
plochu, je barva určena schopností plochy odrážet jednotlivé vlnové délky
dopadajícího světla. V modelu můžeme tuto barvu
definovat velikostí červené, zelené a modré složky. Dopadá-li světlo
pod jiným úhlem, klesá i světelný tok, který na
daný plošný element dopadá. Tok dopadající na plošnou
jednotku segmentu je pak přímo úměrný velikosti průmětu segmentu do roviny
kolmé k dopadajícímu světelnému paprsku (viz obrázek).
V našem
grafickém modelu máme pro každou složku k dispozici 256 hodnot. Definujeme-li
barvu hodnotami R=191; G=127; B=191; znamená to, že
segment odráží 75% dopadající červené a modré a 50% zelené - výsledná barva je fialová. Složky
odraženého světla jsou pak Rcosw, Gcosw, Bcosw. V programovém zpracování
je tedy třeba počítat normálu každého segmentu a její úhel se směrem
dopadajícího světla. Použijeme přitom známých vzorečků (viz procedury
SetVector, VectorProduct a CosAngle v předchozí kapitole)
Konstantní stínování: Stínovaný segment
opět rozdělíme na dva trojúhelníky, Procedurou CosAngle určíme úhel normály
a dopadajícího světla pro každý z nich a barvu výplně určíme vynásobením
barevných složek pro líc resp. rub právě tímto kosinem:
Direct:=CosAngle(u,w);
if Direct>0
then begin
Red:=Trunc(Direct*RightRed);
Green:=Trunc(Direct*RightGreen);
Blue:=Trunc(Direct*RightBlue);
end
else begin
Red:=Trunc(-Direct*WrongRed);
Green:=Trunc(-Direct*WrongGreen);
Blue:=Trunc(-Direct*WrongBlue);
end;
FillTriangle(A,B,C,Red,Green,Blue);
FillTriangle(C,D,A,Red,Green,Blue);
Uvedená metoda je
známa jako konstantní stínování, neboť celý rovinný segment vyplní toutéž
barvou. To je sice nejjednodušší, při použití velkých segmentů však
zdůrazňuje, že „oblý“ povrch tělesa je aproximován
rovinnými segmenty. Tomu se dá předejít buď volbou jiné
stínovací metody, nebo zmenšováním segmentů.
Příklad 1.: Sestavte program pro zobrazování grafů spojitých funkcí metodou konstantního
stínování. Celý příklad je zpracován analogicky jako př.
1. předchozí kapitoly a modifikován dle výše uvedených
sekvencí. Příklad umožňuje uživateli stejně jako v
předchozích případech zadávat rovnici plochy, parametry perspektivního
promítání, barvu pro líc a rub plochy a dále počet segmentů
a tím také jejich velikost. Na přiloženém obrázku
je výstupy z programu, kdy úpočet zadaných segmentů byl v prvním
případě 15, ve druhém 40 a ve třetím 160.
Zde najdete kompletní zdrojový kód
a zde spustitelný kód
Příklad 2.: Sestavte program pro
zobrazování parametricky zadaných ploch metodou konstantního stínování. Celý
příklad je opět zpracován analogicky jako př. 2. předchozí
kapitoly.
Zde najdete kompletní zdrojový kód
a zde spustitelný kód
Drsnost povrchu: reálné objekty nemají nikdy dokonale hladký povrch.
Větší či menší drsnost povrchu plochy se projeví větší či
menší náhodností odrazu dopadajícího paprsku. To lze
zohlednit větším či menším rozptylem barvy při vykreslování jednotlivých
segmentů procedurou DrawSegment. Poslední dva příkazy v proceduře
FillTriangle - MoveTo(h1,i); LineTo(h2,i); které vykreslují
vodorovnou úsečku konstantní barvou, je třeba nahradit postupem po jednotlivých
pixelech. V proceduře je třeba deklarovat proměnné Red,
Green, Blue typu Integer. Pro každý pixel nastavíme tyto hodnoty na uživatelem definovanou barvu a každou složku
rozmažeme proměnnou RoughPixel, kterou nastavujeme randomem vynásobeným
koeficientem Rough-ness, který pro drsnost zadal uživatel. Takto rozmazanou
hodnotu musíme ještě ošetřit proti přetečení:
for
j:=h1 to h2 do
begin
Shade:=2*Round((Random-0.5)*Roughness);
{nastavení rozptylu světla pro daný pixel}
if
Red+Shade>255 then R:=255
else if
Red+Shade<0 then R:=0
{ošetření proti přetečení a rozmazání červené}
else R:=Red+Tone;
...................
{totéž pro Green, Blue}
Draw3D.Image1.Canvas.Pixels[j,i]:=SetColor(R,G,B);
end;
Je-li hodnota Shade pro
každou barevnou složku stejná, nemění se barevný odstín drsné plochy (viz pravá
část výstupu). Měníme-li tuto hodnotu, měníme bod po bodu také barevný odstín,
čímž plocha získává i „perleťový“ vzhled (viz levá
část výstupu).
Na připojeném
obrázku vidíme část anuloidu, zhotoveného z drsného materiálu.
Příklad 3 - studie drsných povrchů ploch zadaných explicitně
Zde najdete kompletní zdrojový kód a zde spustitelný kód
Příklad 4 - studie drsných povrchů ploch zadaných parametricky
Zde najdete kompletní zdrojový kód a zde spustitelný kód
Osvětlení a lesk povrchu: Na začátku kapitoly jsme
konstatovali, že barva segmentu, kterou vnímá pozorovatel, závisí na kosinu úhlu, který svírá jeho normála se směrem
dopadajícího světla (tato hodnota je vyčíslována funkcí CosAngle). Jestliže barevné složky přepočítáváme jinými funkcemi, můžeme simulovat rùznou intenzitu osvětlení a lesk plochy.
Příklad 5, 6: Zde
jsou zprogramovány studie lesku a osvětlení
explicitně a parametricky zadaných ploch. Pro úpravu
intenzity barvy jsou použity dvě funkce. Parametrem Osvětlení (v
programu proměnná Light) měníme exponent funkce
. Ten nemusí být celočíselný, nebot´ funkce je vyčíslována
logaritmicky - tosv:=exp(Light*ln(tosv)). Pro změnu
lesku je použita exponenciální funkce 1-exp(-1/sqr(Shine*tosv-pi/2)),
kde parametr Shine zadává uživatel. Na připojeném obrázku vidíme výstup, kde
můžeme srovnat různě osvětlené a různě matné části
kulové plochy.
Studie
lesku a osvětlení pro funkce dvou proměnných
kompletní zdrojový kód
spustitelný kód
Plochy
zadané parametrickými rovnicemi
kompletní zdrojový kód
spustitelný kód
Interpolace stínu: Jak již bylo řečeno,
konstantní stínování nežádoucím způsobem zvýrazňuje hrany. Jedním
ze způsobů, jak tomu předejít, je interpolace stínu. Interpolujeme-li sestrojovanou plochu jednotlivými segmenty tak,
jak bylo popsáno výše, pak tato plocha prochází každým vrcholem libovolného
segmentu. Deklarujme v programu segmenty plochy takto:
Type TSegment = record A,
B, C, D:T3DPoint;
ShadeA,ShadeB,ShadeC,ShadeD,
Dist :Double;end;
var
Segment :array [0..50000] of
TSegment;
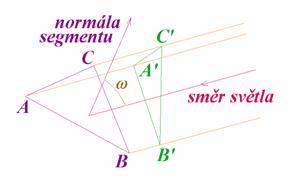
Při interpolaci
stínu stojíme v první řadě před úkolem určit přibližně směr normály hledané
plochy ve společném vrcholu čtyř interpolujících segmentů. Interpolující
segment není obecně rovinný a
lze v něm získat celkem čtyři normály - normálové vektory rovin trojúhelníků
,
, 
, 
. Označme společný vrchol čtyř sousedních segmentů
. Segmenty očíslujme a jejich vrcholy
popišme dle připojeného obrázku. Bod pak inciduje s
body Segment[1].C, Segment[2].D, Segment[3].B a Segment[4].A. Konstrukce normály sestrojované plochy v
bodě je pak zřejmá z
následující sekvence:
With Segment[1] do
begin
SetVector(C,B,u);SetVector(D,C,v);
VectorProduct(u,v,w);
end;
With
Segment[2] do
begin
SetVector(D,A,u);SetVector(D,C,v);
VectorProduct(u,v,w);
end;
With
Segment[3] do
begin
SetVector(B,A,u);SetVector(B,C,v); VectorProduct(u,v,w);
Normal[1]:= Normal[1]+w[1];
Normal[2]:= Normal[2]+w[2];
Normal[3]:= Normal[3]+w[3];
end;
With
Segment[4] do
begin
SetVector(A,B,u);SetVector(A,D,v);
VectorProduct(u,v,w);
Normal[2]:= Normal[2]+w[2];
Normal[3]:= Normal[3]+w[3];
end;
Vrcholům jednotlivých
segmentů, které incidují s bodem pak přiřadíme
zastínění dle kosinu úhlu, který svírá tato normála se světelným paprskem:
Segment[1].ShadeC:=CosAngle(Normal,DirectOfLight);
Segment[2].ShadeD:=Segment[1].ShadeC;
Segment[3].ShadeB:=Segment[1].ShadeC; Segment[4].ShadeA:=Segment[1].ShadeC;
Plocha na připojeném obrázku je sestrojena
pomocí velkých segmentů. Levá část konstantním stínováním, pravá pak pomocí
interpolace stínu.
Příklad 7, 8: Zde je zprogramována
interpolace stínu pro
plochy zadané explicitně: zde
najdete kompletní
zdrojový kód
a zde spustitelný
kód
a parametricky:
zde
najdete kompletní
zdrojový kód
a zde spustitelný
kód
Pro plochy zadané rovnicí je výpočet normál
potřebných pro interpolaci stínu velmi jednoduchý, neboť normálu této plochy
lze s dostatečnou přesností nahradit gradientem funkce .
Příklad 9: Zde je zprogramována
interpolace stínu pro plochu .
Zde najdete kompletní zdrojový
kód a zde spustitelný
kód
Nanášení textur
Povrch reálných předmětů má
také málokdy konstantní barvu. Různobarevnost plochy vyjádříme nejlépe nanesním
textury. Texturou rozumíme funkci, která přiřazuje bodům roviny hodnotu
modulované veličiny, v našem případě barvy: , kde
pro
spojitý a 
pro diskrétní případ. Aplikaci této textury na
povrch tělesa provedeme definováním tzv. mapovací funkce
, která každému bodu z definičního oboru textury
přiřadí bod na povrchu tělesa. Barva
tohoto bodu je pak definována hodnotou textury
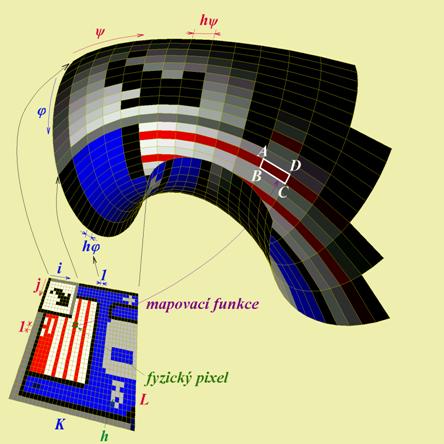
. Definiční obor textury se skládá z fyzických
pixelů, tj. logických čtverců o straně 1 (ve světových souřadnicích).
Mapovací funkcí přiřadíme každému pixelu textury segment námi sestrojované
plochy. Měla by měla být prostá, protože v programové realizaci
potřebujeme většinou obrácený postup – dle parametrizace texturované plochy
procházíme segment po segmentu a každému z nich přiřazujeme barvu
z textury. Mapovací funkce není určena jednoznačně. Tvoří-li povrch tělesa
jediná analytická plocha, je nejjednoduší volit jako mapovací funkci přímo
parametrizaci plochy. Texturu můžeme definovat buď matematickým předpisem
(nejčastěji u jednoduchých pravidelných textur), nebo tabulkou hodnot
(nejlépe ve formě obrazu).
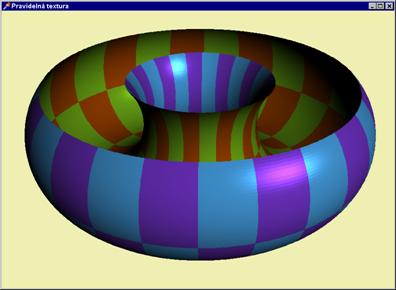
Příklad 1: Aplikujme šachovnicovou texturu
na parametricky zadanou plochu: Mapování zde provádíme pomocí pole proměnných
typu TSegment:
TSegment
= record v,r,s :double; Vert,Horiz:Integer; end;
což jsou segmenty, ze
kterých je plocha sestrojena. Segment je určen hodnotami parametrů
r, s pro vrchol A, hodnota v udává jeho vzdálenost od
pozorovatele (pro řešení viditelnosti. Samotná plocha je pak deklarována jako
pole segmentů:
if (odd(Segment[Index].Vert div GreatOfSquare) and
odd(Segment[Index].Horiz
div GreatOfSquare)) or
(not odd(Segment[Index].Vert div GreatOfSquare) and
not odd(Segment[Index].Horiz div
GreatOfSquare))
then begin
RedSegm:=RightRed;
GreenSegm:=RightGreen;
BlueSegm:=RightBlue;
end
else begin
RedSegm:=WrongRed;
GreenSegm:=WrongGreen;
BlueSegm:=WrongBlue;
end;
Složky barev čtverců jsou definovány proměnnými Right- resp Wrong-, rub
plochy je obarven negativem.
zde najdete kompletní zdrojový kód a zde spustitelný kód
Nanášením obecných
nepravidelných textur můžeme poměrně věrně imitovat materiál, ze kterého je
těleso či plocha zhotovena. Velmi zajímavé výsledky můžeme získat také tehdy,
použijeme-li jako texturu fotografii, či jiný zajímavý obrázek.
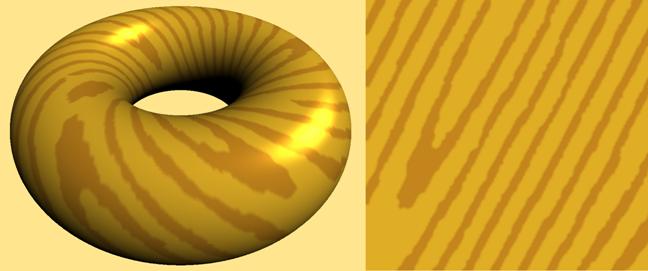
Příklad. 2: Zde je
aplikována obecná textura na anuloid. V prvním případě je imitováno dřevo.
Textura je definována pomocí obrazu. Největším problémem je zde vytvoření
„věrohodné“ předlohy. Ta může být vytvořena uměle pomocí výtvarných technik
nebo sejmutím skutečného povrchu daného materiálu. Ve druhém případě je textura
získána fraktálními technikami, o kterých pojednává následující kapitola
(zde se jedná o detail tzv. Mandelbrotovy množiny). Segmentace plochy je
vždy volena podle textury, a to tak, že každý bod definičního oboru
textury odpovídá právě jednomu segmentu plochy. Mapovací funkce je opět dána
přímo parametrizací plochy.
zde najdete kompletní zdrojový kód a zde spustitelný kód
Nanášení textur však
neslouží jen účelům návrhářským či uměleckým, ale má také významná využití
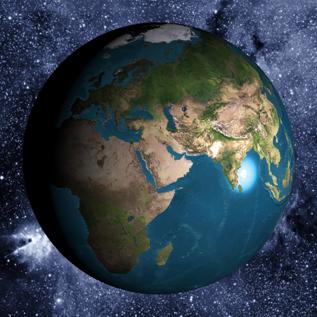
technická. Významné využití poskytuje kartografie. Kartografové řeší většinou
problém opačný - totiž rozvinutí zemského povrchu do roviny. Z grafického
hlediska je naše Země (přibližně) koule, na které je nanesena textura. Rovinná
mapa je vlastně textura, kterou máme nanést na kouli. Máme-li obdélníkovou mapu
světa, můžeme si s našimi současnými znalostmi vyrobit zeměkouli. Princip
je stejný jako v př. 2. Nanášení textury probíhá v cyklu. Výsledkem
jednoho jeho průběhu je jeden obrázek, který uložíme jako jedno okénko
budoucího filmu. Součástí názvu by mělo být i číslo snímku, které pak
usnadní cyklus čtení. Jednotlivé snímky se liší otočením o úhel 360/n (
u koule toho můžeme docílit pouhým posunutím nanášené textury). Takto
vytvořený film pak promítáme jiným programem, který v cyklu pro n=0..51
provede jednu otáčku zeměkoule tím, že vždy zjistí, který obrázek má být
promítnut, pošle ho na kreslící plochu a okamžitě přechází na další
snímek. Vytvoření jednotlivých snímků je sice časově náročné, „film“ zabírá
hodně místa na disku, přesto si ale myslím, že výsledek stojí za to.
Zde najdete kompletní zdrojový kód
a zde spustitelný kód.
Popsané algoritmy
nanášení textury jsou sice poměrně jednoduché, zato však bohužel dosti pomalé.
Náš program zpomaluje především vyčíslování rovnic z řetězce zadaného
uživatelem. Reprezentace fyzických pixelů textury segmenty plochy vyžaduje
poměrně velký počet segmentů, poměrně pomalé je také jejich vyplňování, použitý
Painter's algorithm pro řešení viditelnosti bohužel také není
z nejrychlejších (velká část obrazu se počítá a kreslí zbytečně,
protože bude později překreslena). Relativní jednoduchost použitých algoritmů
je prostě zaplacena pomalejším provedením. Na Control panelu je třeba nejdříve
nahrát zvolenou texturu tlačítkem Loading, poté spustit vlastní nanášení
tlačítlem Start.
Pro speciální plochy
(např. kulová plocha, válcová plocha aj.) lze nanášení textury podstatně
urychlit postupem, který je popsán v matematických podrobnostech
Vržený stín
Kromě vlastního stínu,
který vzniká v důsledku různého úhlu normál segmentů plochy
a dopadajícího světla, existuje stín vržený. Nachází-li se těleso mezi
zdrojem světla a zbytkem scény, pak tuto část scény zastíní. Jednoduché
řešení vržených stínů jsme již předvedli pomocí osové afinity. Toto řešení
umožňuje zadat tvar stínu, aniž bychom cokoli věděli o zdroji světla, díky
jemuž stín vzniká. Situace však většinou bývá opačná: známe zdroj světla
a z něj potřebujeme odvodit stín. Řešení vržených stínů může být
dosti komplikované (těleso může např. zastiňovat i část sebe sama).
Podíváme se na nejjednodušší případ, kdy těleso osvětlené jedním bodovým
zdrojem vrhá stín na vodorovné pozadí. Světelný paprsek je jednoznačně určen
směrovým vektorem , kde
je světelný
zdroj (v programu označen jako LightSource) a 
je bod na povrchu tělesa. Ten pak vrhne stín 
na další
součást scény, která stojí světelnému paprsku v cestě. Jak již bylo
řečeno, budeme předpokládat rovinné vodorovné pozadí. Bod vypočteme
tedy jako průsečík světelného paprsku s rovinou 
(v
připojené proceduře je tato proměnná pojmenována Depth).
Procedure PointShadow(A:T3DPoint;var Ac:T3DPoint);
begin
With
Draw3D do
begin
t:=-(LightSource[3]-Depth)/(A[3]-LightSource[3]);
Ac[1]:=LightSource[1]+(A[1]-LightSource[1])*t;
Ac[2]:=LightSource[2]+(A[2]-LightSource[2])*t;
Ac[3]:=-Depth;
end;
end;
Plocha je segmentována
stejně jako v př. 2 kpt. 8.1. Segment plochy určený vrcholy (které musí postupně
projít procedurou PointShadow) vrhá pak stín určený vrcholy
(které jsme postupně
obdrželi jako výstupy z této procedury). Stín budeme sestrojovat pomocí
procedury FillTriangle použitím černé barvy na bílé
pozadí. Protože tato procedura pracuje s objektem Image,
musíme si obsah původního podkladu před stínováním uschovat.
Pracujeme-li s maticí Canvas, můžeme deklarovat dvojrozměrné pole prvků typu
DWord a matici nazvat např. Ground. Pak ji můžeme
naplnit napři takto:
for
i:=0 to Image.Width-1 do
for j:=0 to Image. Height-1 do
Ground[i,j]:=Image.Canvas.Pixels[i,j];
V případě práce s obrazovými
řádky je lépe k tomuto účelu využít jako paměti pomocný obraz (v Graph3D je k
tomuto účelu k dispozici MemoryImage, který byl již rovněž zmiňován). Je třeba mít deklarovány dvě proměnné jako ukazatele na obrazový řádek,
např:
var SL,
MemSL:PByteArray;
Samotné uschování obrazu pak vypadá takto:
for j:=0 to Image.Height-1 do
begin
SL :=Image.Picture.Bitmap.ScanLine[j];
SLMem:=MemoryImage.Picture.Bitmap.ScanLine[j];
for i:=0 to Image.Width-1 do
begin
Adr:=3*i;
SLMem[Adr]:=SL[Adr];
SLMem[succ(Adr)]:=SL[succ(Adr)];
SLMem[succ(succ(Adr))]:=SL[succ(succ(Adr))];
end;
end;
Kreslicí plochu Image pak můžeme vymazat a
sestrojit do ní černou barvou stín:
for i:=0 to NoOfSegments do
With Segment[i]
do
begin
PointShadow(A,Ac);PointShadow(B,Bc);PointShadow(C,Cc);PointShadow(D,Dc);
Draw3D.FillTriangle(Ac,Bc,Cc,0,0,0);Draw3D.FillTriangle(Cc,Dc,Ac,0,0,0);
end;
Dále porovnáváme bod po bodu obrazy Image a MemoryImage. Je-li bod na Image bílý, obarvíme ho původním pozadím, je-li černý,
původnímu pozadí poněkud snížíme jas, např. vhodně zvolenou konstantou Brightness z intervalu 
. Při práci na pozadí (Canvas) můžeme postupovat
např. takto:
for i:=0 to Image.Width-1 do
for j:=0
to Image. Height-1 do
if Image.Canvas.Pixels[i,j]=clWhite
then
Image.Canvas.Pixels[i,j]:=MemoryImage.Canvas.Pixels[i,j]
else begin
With MemoryImage.Canvas do
begin
Blue:=Pixels[i,j]
div (256*256);
Green:=(Pixels[i,j-256*256*Blue)
div 256;
Red:=Pixels[i,j]-256*256*Blue-256*Green;
end;
Red:=Round(Brightness*Red);
Green:=Round(Brightness*Green);
Blue:=Round(Brightness*Blue);
Image.Canvas.Pixels[i,j]:=
Red+256*Green+256*256*Blue;
end;
Práce v obrazových řádcích:
for j:=0 to Image.Height-1 do
begin
SL :=Image.Picture.Bitmap.ScanLine[j];
SLMem:=MemoryImage.Picture.Bitmap.ScanLine[j];
for i:=0 to Image.Width-1 do
begin
Adr:=3*i;
if (SL[Adr]=255) and (SL[succ(Adr)]=255) and
(SL[succ(succ(Adr))]=255)
then begin
SL[Adr]:=SLMem[Adr];
SL[succ(Adr)]:=SLMem[succ(Adr)];
SL[succ(succ(Adr))]:=SLMem[succ(succ(Adr))];
end
else begin
SL[Adr]:=Round(Brightness*SLMem[Adr]);
SL[succ(Adr)]:=Round(Brightness*SLMem[succ(Adr)]);
SL[succ(succ(Adr))]:=Round(Brightness*SLMem[succ(succ(Adr))]);
end
end;
end;
Při konstrukci připojeného obrázku byl stín navíc poněkud rozmazán
obrazovým filtrem typu dolní propust, čímž jsou simulovány nenulové rozměry
světelného zdroje a dále započten úbytek intenzity světla se vzrůstající vzdáleností.
Zde najdete kompletní zdrojový kód a zde spustitelný kód
Průhledné plochy
Dosud jsme
předpokládali, že objekty, které sestrojujeme, jsou neprůhledné
a neprůsvitné, tj. že dopadající světlo je odraženo popř. pohlceno
a žádné neprochází. Pro řadu objektů však tento předpoklad nemusí vždy
platit. Průhledným
objektem přitom rozumíme objekt, kterým se světlo šíří podle zákonů
geometrické optiky, tj. uvažujeme pouze odraz a lom světla, event úbytek
intenzity v závislosti na vzdálenosti. Průsvitným objektem rozumíme objekt,
kde je třeba brát v úvahu i vlnovou podstatu světla, projevující se
především jeho ohybem. Při algoritmizaci nelze bohužel většinou postihnout celý
popsaný fyzikální proces. Jednak pro celkovou složitost a jednak pro
nedostupnost potřebných informací. U každého paprsku by totiž bylo třeba
propočítat všechny odrazy a lomy a barvy interferujících paprsků
míchat. Navíc by bylo třeba započítat další jevy - absorbci, difuzi, dispersi
apod. To ovšem lze udělat pouze pro objekt, který lze popsat analyticky
a pro jehož každý bod jsou tyto veličiny známy. Většina objektů (např.
mikroskopovaný biologický preparát) těmto požadavkům ani přibližně nevyhovuje.
Přesto je možné dosti uspokojivě vzhled takového objektu popsat tak, že budeme
uvažovat vždy jen poměr intenzit odraženého a lomeného paprsku. Ostatní
veličiny - změna směru vlivem lomu, difuzi, dispersi apod. - nebudeme uvažovat.
Vpodstatě to znamená, že budeme prozatím uvažovat pouze nekonečně tenké průhledné plochy.
Za výše uvedených
zjednodušujících předpokladů není programová realizace příliš složitá. Plochu
tentokrát sestrojujeme pomocí průhledných segmentů. Jejich vrcholy
je třeba promítnout do průmětny a pak je možno použít výše zmíněnou proceduru
FillTriangle2D, je však třeba modifikovat řádky označené tam jako {sestrojení úsečky}.
Procedura FillTriangle2D, jak již bylo uvedeno, vyplní celý trojúhelník
konstantní barvou. V případě průhledného či průsvitného
povrchu je však třeba barvu každého pixelu míchat minimálně ze dvou barev -
barvy odraženého a prošlého světla. Předmětné řádky kódu
For i:=h1 to h2 do
begin
Adr:=3*i;
ScanRow[Adr]:=Blue;
ScanRow[succ(Adr)]:=Green;
ScanRow[succ(succ(Adr))]:=Red;
end;
sestrojí ve fyzické
rovině vodorovnou úsečku spojující fyzické pixely o souřadnicích ;
, a to konstantní barvou, která je dána konstantními
hodnotami barevných složek Red, Green, Blue (barva odraženého světla). Tuto barvu je však nyní potřeba smíchat s barvou světla prošlého,
a to pixel po pixelu a složku po složce. V řešeném příkladu je
prošlé, odražené i složené světlo deklarováno jako záznam tří barevných
složek - record
Red, Green,Blue:Byte;end. Barva odraženého světla je určena barvou texturz, barvu
prošlého světla budeme modelovat pomocí pixelu, který je překreslován.
Intenzita prošlého resp. odraženého světla je uložena v proměnné Int_P
resp Int_O:
for
i:=h1 to h2 do
begin
Adr:=3*i;
With
Michane do
begin
Red:=Trunc((Int_P*Prosle[i,j].Red
+Int_O*Odrazene[i,j].Red)/(Int_P+Int_O));
Green:=Trunc((Int_P*Prosle.Green[i,j]
+Int_O*Odrazene[i,j].Green)/(Int_P+Int_O));
Blue:=Trunc((Int_P*Prosle.Blue[i,j]
+Int_O*Odrazene[i,j].Blue)/(Int_P+Int_O));
ScanRow[Adr]:=Blue;
ScanRow[succ(Adr)]:=Green;
ScanRow[succ(succ(Adr))]:=Red;
end;
end;
Příklad 1.: Dutá průhledná zeměkoule. Zde je naprogramován povrch zeměkoule tak, jak by vypadal v
případě, že by byl nahrazen nekonečně tenkou průhlednou kulovou plochou.
Zde najdete kompletní zdrojový kód
a zde
spustitelný kód
Příklad 2.:
Průhledná plocha zadaná rovnicí . V kpt. 8.2. jsme popisovali sestrojení plochy
zadané rovnicí a v kpt.
8.3. jsme ji sestrojili pomocí interpolace stínu (viz. kpt. 8.3. př. 9). Zde je
plocha sestrojena pomocí průhledných segmentů dle výše uvedeného algoritmu.
Zde najdete kompletní zdrojový kód
a zde
spustitelný kód