Cvičení 9: Delphi - kreslení křivek, křivky technické praxe

1  Kreslení křivek

1.1  Obecný postup

Metoda úseček - rozdělí se interval osy x na stejné dílky a funkční hodnoty v krajních bodech jednotlivých dílku se spojí úsečkou

1.2  Jednoduchý program

Program, který vykreslí explicitní funkci y=x2+2x+1 a po zašktnutí políčka také osy souřadnic.
1. Umístěte na formulář tři Buttony a jeden CheckBox.
2. Buttony popište Smazat, Kresli, Konec, políčko Zobrazit osy.
3. Propojte buttony Smazat a Konec se známými procedurami.
4. K Buttonu Kresli přidejte proceduru kresli a dopište zdrojový kód, který popisuje předchozí postup kreslení křivky pomocí lomených čar. 
procedure TControlPane.kresli(Sender: TObject);
var hx,x1,x2,y1,y2:real;
    PocetUseku:integer;
    A,B:TPoint;
    Red,Green,Blue:Byte;

function f(x:real):real;
begin
  f:=x*x+2*x+1;
end;

begin
  with Image1 do
  begin
    //definicni obor a obor hodnot
    x1:=-10; x2:=10;
    y1:=-10; y2:=10;
    PocetUseku:=150;
    hx:=(x2-x1)/PocetUseku;
    // barva
    Red:=0;
    Green:=0;
    Blue:=200;

    //prevod  na uzivatelske souradnice
    Scale(x1,x2,y1,y2);
    //vykresleni os
    if CheckBox1.checked=true then
    begin
      XAxis(x1,x2,0,Red,Green,Blue);
      YAxis(y1,y2,0,Red,Green,Blue);
    end;
   // metoda usecek
    A[1]:=x1;
    A[2]:=f(x1);
    Repeat
      B[1]:=x1+hx;
      B[2]:=f(x1+hx);
      Line(A,B,0,150,0);
      A:=B;
      x1:=x1+hx;
    until x1>x2;
   end;
end;

2  Křivka se zadávanými parametry

- rozšíříme předchozí program o zadávání barev a rozsahu souřadných os
  1. přidejte 7 edit boxů a připište doplňující text podle obrázku
  2. smažte zadávání barvy a souřadných os ve zdrojovém kódu
  3. převeďte všechny texty v edit boxech na čísla pomocí funkce VAL, připište proměnnou chyba typu integer do deklarace proměnných(var chyba:integer)
    Val(políčko z formuláře, proměnná kam se uloží číslo, chybová hláška);
            Val(EditBox1.text, x1, chyba);


    Val(Edit1.text, x1, chyba);
Val(Edit2.text, x2, chyba);
Val(Edit3.text, y1, chyba);
Val(Edit4.text, y2, chyba);
Val(Edit5.text, Red, chyba);
Val(Edit6.text, Green, chyba);
Val(Edit7.text, Blue, chyba);
  4. Poznámka: inverzní funkce k VAL je funkce STR(číslo na převod, proměnná typu String kam se číslo uloží); V následujícím příkladu se číslo 150 převede do proměnné cislo typu string a EditBox 1 vypíše tuto hodnotu. 
    var cislo:string;
begin
str(150, cislo);
Edit1.text=cislo;
end;

3  Bézierovy, Coonsovy a Fergusonovy křivky

Vytvořte program, který po zaškrtnutí příslušného edit boxu vykreslí Bezierovu, Coonsovu nebo Fergusonovu křivku. Z panelu se bude zadávat rozsah os, barva křivky a její typ. (viz. obrázek)
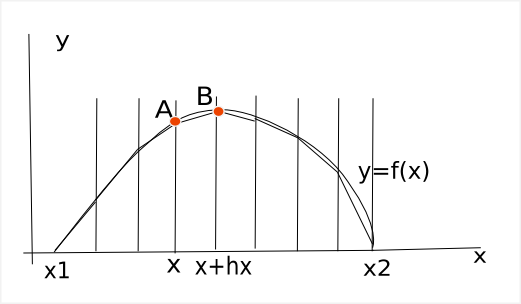
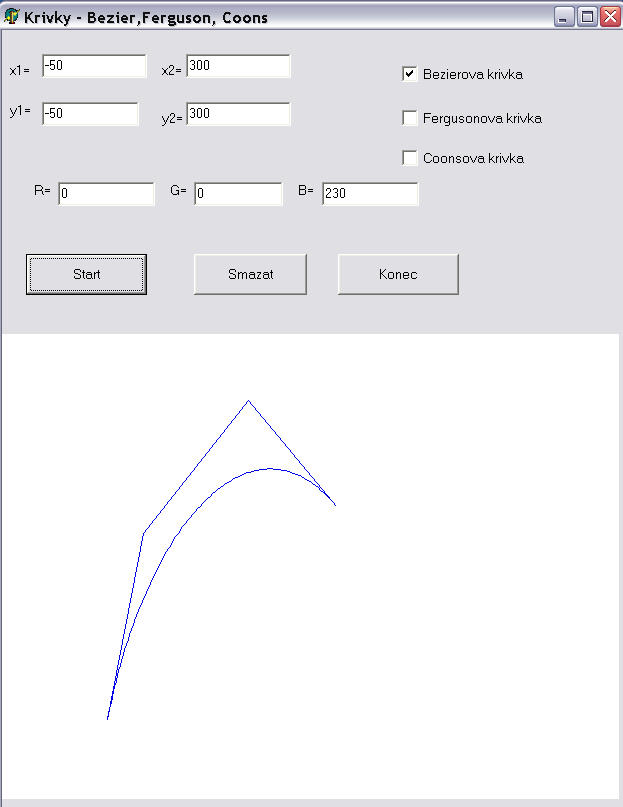
  1. Vytvořte si adresář Bezier a do něj vložte stažené zdrojové kódy (stejně jako v minulém cvičení)
  2. Vytvořte panel podle předlohy, nastavte hodnoty EditBoxu na odpovídající čísla
  3. Buttony Konec a Smazat propojte s odpovídajícími procedurami
  4. K buttonu Kresli propojte OnClick proceduru kresli
  5. Nadeklarujte pomocné proměnné 
    var Red,Green, Blue:byte;
    x1,x2,y1,y2,ht,t:real;
    chyba,i:integer;
    P,C:TArrayOfPoints;
  6. Nadefinujte proceduru Bezier uvnitř procedury kresli (před begin) 
    procedure Bezier(t:real; var A:TPoint);
begin
 A[1]:=P[0,1]*(1-t)*(1-t)*(1-t)+
       P[1,1]*3*t*(1-t)*(1-t)+
       P[2,1]*3*t*t*(1-t)+
       P[3,1]*t*t*t;

 A[2]:=P[0,2]*(1-t)*(1-t)*(1-t)+
       P[1,2]*3*t*(1-t)*(1-t)+
       P[2,2]*3*t*t*(1-t)+
       P[3,2]*t*t*t;
end;
  7. Za begin doplňte převod textů z EditBoxu na čísla pomocí funkce VAL, nastavte uživatelské souřadnice procedurou Scale a zadejte řídící body pro křivky. 
    Val(Edit1.text, x1, chyba);
Val(Edit2.text, y1, chyba);
Val(Edit3.text, x2, chyba);
Val(Edit4.text, y2, chyba);

Val(Edit5.text, Red, chyba);
Val(Edit6.text, Green, chyba);
Val(Edit7.text, Blue, chyba);
Scale(x1,x2,y1,y2);

P[0,1]:=10;  P[0,2]:=10;
P[1,1]:=30;  P[1,2]:=150;
P[2,1]:=90;  P[2,2]:=250;
P[3,1]:=140; P[3,2]:=170;
  8. Vykreslete řídící polygon - tj. spojnici řídících bodů 
    with Image1.canvas do
begin
  Line(P[0],P[1],Red,Green,Blue);
  Line(P[1],P[2],Red,Green,Blue);
  Line(P[2],P[3],Red,Green,Blue);
end;
  9. Doplňte vykreslení křivky pomocí procedury Polyline. 
    //bezierova krivka zaskrtnuta
if checkBox1.checked then
begin
  ht:=0.01;
  t:=0;
  i:=1;
  while t<1 do
    begin
      Bezier(t,C[i]);
      i:=i+1;
      t:=t+ht;
    end;
  PolyLine(C,i-1,Red,Green,Blue);
end;
  10. Před begin dopňte další dvě procedury na Coonsovy a Fergusonovy křivky 
    procedure Ferguson(t:real; var A:TPoint);
begin
 A[1]:= P[0,1]* (2*t*t*t-3*t*t+1)+
        P[1,1]*(t*t*t-2*t*t+t)+
        P[2,1]*(t*t*t-t*t)+
        P[3,1]*(-2*t*t*t+3*t*t);

 A[2]:= P[0,2]* (2*t*t*t-3*t*t+1)+
        P[1,2]*(t*t*t-2*t*t+t)+
        P[2,2]*(t*t*t-t*t)+
        P[3,2]*(-2*t*t*t+3*t*t);
end;

procedure Coons(t:real; var A:TPoint);
begin
  A[1]:=1/6*(P[0,1]*(1-t)*(1-t)*(1-t)+P[1,1]*(3*t*t*t-6*t*t+4)+
  P[2,1]*(-3*t*t*t+3*t*t+3*t+1)+
  P[3,1]*(t*t*t));

  A[2]:=1/6*(P[0,2]*(1-t)*(1-t)*(1-t)+P[1,2]*(3*t*t*t-6*t*t+4)+
  P[2,2]*(-3*t*t*t+3*t*t+3*t+1)+
  P[3,2]*(t*t*t));
end;
  11. Analogicky jako v předchozím případě doplňte část na vykreslení. Bude se volat procedura Feguson a Coons a CheckBox bude mít index 2 nebo 3, jinak je vvše úplně stejné.
  12. To je vše, přátelé....


File translated from TEX by TTH, version 3.67.
On 2 Aug 2007, 10:38.