Základní pojmy

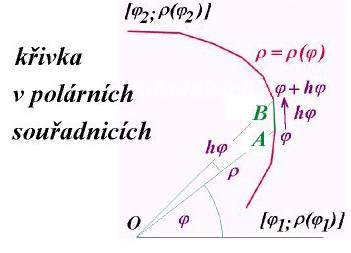
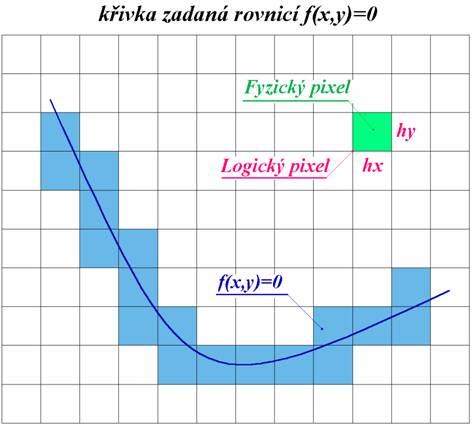
Princip konstrukce spojitých analytických křivek:

Spustit příklad

Spustit příklad

Spustit příklad

Spustit příklad

Známe je z CAD systémů:

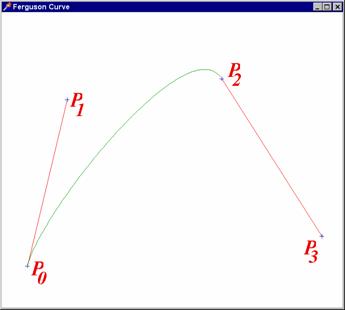
Fergusonovy křivky

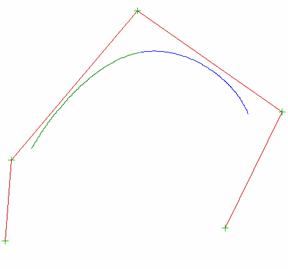
Technická praxe často vyžaduje křivky, určené tzv. řídícími body nebo o řídícím polygonem. Jednu z nejjednodušších takových křivek používal od r. 1964 J. C. Ferguson. Křivka je určena dvěma krajními body , a dvěma tečnými vektory , _. Velikost těchto vektorů ovlivňuje zároveň druhou derivaci křivky (čím je velikost větší, tím více křivka k vektoru „přimyká“). Křivka je definována parametrickými rovnicemi

;

; ; ;

Funkce jsou polynomy 3. stupně, Fergusonova křivka je tedy kubická parabola.

Spustit příklad

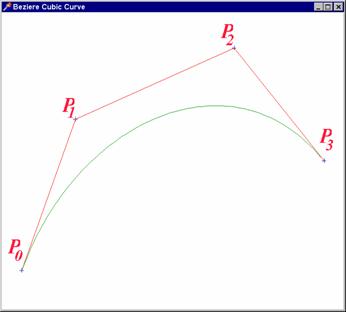
Bézierovy křivky

V letech 1959 - 1962 navrhli nezávisle na sobě P. E. Béziere a P. de Casteljau křivku, která je určena čtyřmi body , , , . Je definována parametrickými rovnicemi

;

; ; ;

Spustit příklad

Hladké napojování – je třeba zajistit společnou tečnu

Spustit příklad

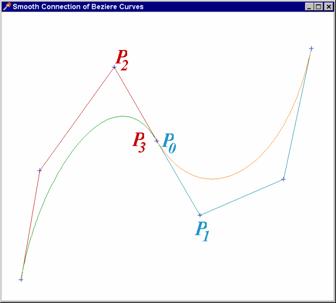
Coonsovy křivky a B-splajny

Další křivky hojně používané v technické praxi definoval S. A. Coons. Coonsova kubika je definována opět čtyřmi řídícími body a kubickými polynomy :

;

; ; ;

Spustit příklad

Hladké napojování – opakování prvních tří bodů řídícího polygonu:

Spustit příklad