Rovinné křivky
Uživatelská souřadná soustava
Jak již víme, DELPHI pracuje
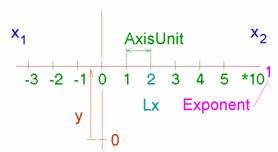
s tzv. světovými souřadnicemi, které jsou na připojeném obrázku vyznačeny
modře. Práce v takové soustavě je pro uživatele značně nepříjemná.
Vytvoříme si proto tzv. uživatelskou souřadnou soustavu, která je vyznačena
červeně. „Délku“ osy ![]() (interval
(interval ![]() ) jakož i „délku“ osy
) jakož i „délku“ osy ![]() (interval
(interval ![]() ) budeme moci měnit. V obrázku je
) budeme moci měnit. V obrázku je ![]() resp.
resp. ![]() délka uživatelské jednotky na ose
délka uživatelské jednotky na ose ![]() resp.
resp. ![]() ve
světových souřadnicích. Zřejmě je
ve
světových souřadnicích. Zřejmě je

![]() ;
;![]() (1)
(1)
Souřadnice uživatelského počátku O ve světových souřadnicích jsou pak
![]() ;
; ![]() (2)
(2)
Je-li pak ![]() libovolný bod na kreslicí ploše,
libovolný bod na kreslicí ploše, ![]() jeho souřadnice
v uživatelské soustavě a
jeho souřadnice
v uživatelské soustavě a ![]() jeho souřadnice
ve světové soustavě, pak zřejmě platí
jeho souřadnice
ve světové soustavě, pak zřejmě platí
![]() ;
; ![]() (3)
(3)
Realizujme nyní uživatelskou
souřadnou soustavu a vykresleme trojúhelník s danými vrcholy. Na formulář
jsme opět umístili objekt Image, proceduru, která trojúhelník vykresluje, jsme
nazvali Triangle
a budeme ji aktivovat OnClick.
unit Graph2D;
interface
uses
Windows, Messages, SysUtils, Classes,
Graphics, Controls, Forms, Dialogs,ExtCtrls;
type
TPoint = array [1..2]
of Double;
TForm1 = class(TForm)
Image1: TImage;
procedure Triangle(Sender:TObject);
private
{ Private declarations }
public
{ Public declarations }
procedure Scale(x1,x2,y1,y2:Double);
function XCoor(x:Double):integer;
function YCoor(y:Double):integer;
end;
Všimněte si však,
že se hlavička této procedury automaticky zapsala také jako nová vlastnost typu
TForm. Tímto
způsobem můžeme i my sami obohacovat typ TForm
o nové proměnné, procedury a funkce, nejlépe do odstavce Public (zde
budou tyto vlastnosti v případě potřeby dostupné i z jiných jednotek).
Nyní se tedy dostáváme k červenému textu, který musíme dopsat sami a kterým realizujeme uživatelskou souřadnou
soustavu.
var Form1
:TForm1;
Unit_X,Unit_Y,x1,x2,y1,y2:Double;
O :TPoint;
implementation
{$R *.DFM}
procedure TForm1.Scale(x1,x2,y1,y2:Double);
begin
Unit_X:= Image1.Width/(x2-x1);
Unit_Y:=Image1.Height/(y2-y1);
O[1]:= -x1*Unit_X;O[2]:=y2*Unit_Y;
end;
function TForm1.XCoor(x:Double):integer;
begin XCoor:=trunc(O[1]+Unit_X*x);end;
function TForm1.YCoor(y:Double):integer;
begin
YCoor:=trunc(O[2]-Unit_Y*y);end;
procedure
TForm1.Triangle(Sender: TObject);
begin
end;
end.
Protože
budeme chtít pracovat s body v rovině, deklarujeme v části Interface typ TPoint jako uspořádanou dvojici reálných čísel (předefinovali
jsme tedy typ TPoint, který je v
Příklad 1:
Výše uvedená část kódu by samozřejmě ještě trojúhelník nevykreslila. Doplňme
jej tak, abychom na výstupu trojúhelník dostali. V řešeném příkladu jsou
podobně jako výše uvedené tři procedury a funkce doplněny další:
procedure
PutPixel(X:TPoint;Color:DWord);
procedure
MoveTo(X:TPoint);
procedure
LineTo(X:TPoint;Color:DWord);
procedure
Line(X,Y:TPoint;Color:DWord);
procedure
XAxis(x1,x2,y:Double;Color:DWord);
procedure
YAxis(y1,y2,x:Double;Color:DWord);
Procedury PutPixel, MoveTo a LineTo fungují analogicky, jako metody
obsažené v TCanvas ve standardním
procedure
TForm1.LineTo(X:TPoint;Color:DWord);
begin
With
Image1.Canvas do
Begin
Pen.Color:=Color;LineTo(XCoor(X[1]),YCoor(X[2]));
end;
end;
V těchto procedurách tedy není využit přístup
do bitmapy přes obrazové řádky tak, jak bylo uvedeno v matematických
podrobnostech předchozí kapitoly. V dalším textu budeme
prozatím používat osmibitové barvy, resp. předdeklarované konstanty - např.
slRed, slGreen atd., které byly popsány v
matematických podrobnostech předchozí kapitoly, a vlastní proceduru Line pro
úsečku, která je popsána v matematických podrobnostech této kapitoly .
Jsou-li k dispozici výše uvedené
procedury, pak trojúhelník vykreslíme velmi jednoduše:
procedure
TForm1.Triangle(Sender: TObject);
var A,B,C:TPoint;
begin
A[1]:=-2;A[2]:=6;
B[1]:= 4;B[2]:=-1; C[1]:= 5;C[2]:=5;
{definice vrcholů}
x1:=-4;x2:=7;y1:=-3;y2:=8;
Scale(x1,x2,y1,y2);
{definice uživatelské kreslicí plochy}
Line(A,B,slRed);Line(B,C,slRed);Line(A,C,slRed); {vlastní
konstrukce}
end;
Zde
najdete kompletní zdrojový
kód a zde spustitelný kód
Příklad 2: Předchozí příklad vylepšíme o cejchování
souřadných os, který obstarávají procedury
XGauge (x1,x2,y:Double;Color:Byte);
resp. YGauge
(y1,y2,x:Double; Color: Byte). Podle velikosti měřítka procedury
zvolí vhodnou velikost jednotky na popis, k popisu připojí vzdálenost
sousedních „fousů“. Fungují následujícím způsobem (jako příklad uveďme popis
osy x):
procedure TForm1.XScale(x1,x2,y:Double;Color:DWord);
var AxisUnit :Double;
Text :String;
Lx,Exponent :Integer;
begin
Image1.Canvas.Font.Color:=Color;
AxisUnit:=1E30;Lx:=0;Exponent:=30;
While (x2-x1)/AxisUnit<1 do
begin
AxisUnit:=AxisUnit/10;Exponent:=Exponent-1;
end; {nalezení vhodné velikosti jednotky}
if x1<0 {nalezení
nejmenší popisky}
then Repeat Lx:=Lx-1 Until
AxisUnit*(Lx-1)<x1
else Repeat Lx:=Lx+1 Until AxisUnit*(Lx+1)>x1;
With Image1.Canvas do
repeat
MoveTo(XCoor(AxisUnit*Lx),YCoor(y)-3); {cejchování osy}
LineTo(XCoor(AxisUnit*Lx),YCoor(y)+3);
Str(Lx,Text);TextOut(XCoor(AxisUnit*Lx),YCoor(y)+5,Text);Lx:=Lx+1; {popisky}
until
AxisUnit*Lx>x2;
Str(Exponent,Text); {funkce Str převádí číselnou hodnotu na řetězec}
Image1.Canvas.TextOut(XCoor(x2)+15,YCoor(y)+5,'*10');
{jednotka
a exponent}
Image1.Canvas.TextOut(XCoor(x2)+35,YCoor(y),Text);
end;
Zde najdete kompletní zdrojový
kód a zde spustitelný kód
Předchozí příklady neumožňují měnit parametry za běhu programu. Tento nedostatek napravíme v následujícím příkladu.
Příklad 3: K ovládání našeho formuláře Form1 založíme celý nový formulář. V menu File klikneme na New Form. Objeví se nám nový formulář Form2 spolu s novou jednotkou Unit2. Tomuto formuláři změníme titulek na Control Panel. a umístíme na něj tři tlačítka, která vybereme ze stránky Standard vícestránkové lišty. Těmto tlačítkům změníme titulky na „Start“, „Clear Image“ a „Exit“. Dále několik objektů Static Text, tento typ najdeme v liště Additional, jejichž titulky budou „Triangle“, „Scale“, další budou sloužit pro popis vrcholů - „A=“, „B=“, „C=“ a uživatelských rozměrů kreslicí plochy „x“, „y“. Dále zde umístíme Check Box (lišta Standard) s titulkem „Show Axses“, s jehož pomocí bude uživatel vybírat možnost zobrazení souřadných os. O tom, zda se souřadné osy mají či nemají zobrazit, rozhoduje vlastnost Checked typu Boolean. Konečně přidáme potřebný počet objektů Edit (opět v liště Standard), do kterých bude uživatel zadávat hodnoty. Změníme jejich jména (vlastnost Name v Object Inspectoru) na EditA1, EditA2, …, resp EditX1, EditX2…, a Text, tak, aby při spuštění programu tato okna obsahovala výchozí parametry. Náš formulář vypadá tak, jak vidíme na přiloženém obrázku. Procedury týkající se rovinné uživatelské souřadné soustavy jsou v samostatné jednotce - původní Unit1 přejmenujeme na Graph2D pomocí File/SaveAs. Do této jednotky jsme také umístili objekt typu TImage, který jsme nazvali Draw2D a všechny konstrukce probíhají v tomto objektu. Např. procedura pro mazání kreslicí plochy kreslí přes celou tuto plochu bílý obdélník:
procedure TDraw2D.ClearImage;
begin
with Image1.Canvas do
begin
Pen.Color:=clWhite;Brush.Color:=clWhite;end;
with Image1 do Canvas.Rectangle(0,0,Width-1,Height-1);
end;
V Control Panelu nejdříve zařídíme čtení parametrů z Edit-okének, a to procedurou Setting:
Procedure TControl_Panel.Setting;
var Code:Integer;
begin
With
Draw2D do
begin
Val(EditA1.Text,A[1],Code);
Val(EditA2.Text,A[2],Code);
Val(EditY2.Text,y2,Code);
Scale(x1,x2,y1,y2);
end;
end;
Tlačítka v Control Panelu spojíme přes událost OnClick pořadě s procedurami Triangle, ClearImage a Exit:
procedure TControl_Panel.Triangle(Sender: TObject);
begin
With Draw2D do
begin
ClearImage;Setting;
if CheckBox1.Checked then CoorSystem(slRed);
Line(A,B,slBlue);Line(B,C,slBlue);Line(A,C,slBlue);
end;
end;
procedure TControl_Panel.ClearImage(Sender: TObject);
begin Draw2D.ClearImage;end;
procedure TControl_Panel.Exit(Sender: TObject);
begin Halt; end;
V příkladu je navíc řešeno zadávání vrcholů trojúhelníka myší
Zde najdete kompletní zdrojový
kód a zde spustitelný kód
Křivky
typu ![]()
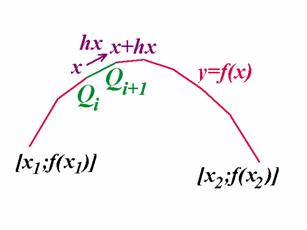
Z hlediska konstrukce se jedná o nejjednodušší křivky. Lze je konstruovat jako lomené čáry složené z úseček dle připojeného obrázku:
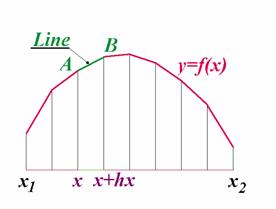
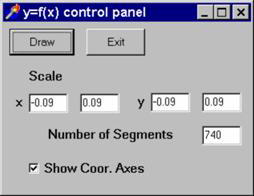
Příklad 1: Sestrojme proceduru
Explicit_Curve, která sestrojí graf funkce ![]()
![]() (viz připojený výpis). Nejdříve opět
sestavíme ovládací panel ze známých komponent (v panelu NumberOfSegments bude
uživatel zadávat počet segmentů, z kterých má být křivka sestrojena. Stejně
jako v předchozí kapitole sestrojíme uživatelskou kreslicí plochu,
souřadné osy a definujeme barvu sestrojované křivky. Vidíme, že funkce
(viz připojený výpis). Nejdříve opět
sestavíme ovládací panel ze známých komponent (v panelu NumberOfSegments bude
uživatel zadávat počet segmentů, z kterých má být křivka sestrojena. Stejně
jako v předchozí kapitole sestrojíme uživatelskou kreslicí plochu,
souřadné osy a definujeme barvu sestrojované křivky. Vidíme, že funkce ![]() je definována uvnitř procedury. Vlastní konstrukce spočívá v nastavení
kroku hx a v postupné konstrukci úseček
je definována uvnitř procedury. Vlastní konstrukce spočívá v nastavení
kroku hx a v postupné konstrukci úseček ![]() :
:
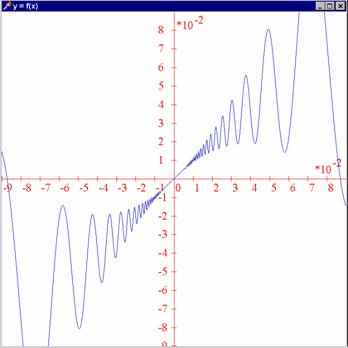
Procedure
TControl_Panel.Explicit_Curve(Sender:TObject);
var x,hx:Double;
A,B :TPoint;
function f(x:Double):Double;
begin if x=0 then f:=0
else f:=x+10*x*x*sin(1/x); end;
begin
With Draw2D do {Uživatelská kreslicí plocha}
begin
if CheckBox1.Checked then
begin {souřadné osy a
jejich popis}
XScale(x1,x2,0,clRed); {sestrojí stupnici rovnoběžnou s osou x, resp. y.}
YScale(y1,y2,0,clRed); { Pro určení barvy je použita standardní konstanta }
end; { kvůli snazšímu
popisu os pomocí procedury TextOut}
hx:=(x2-x1)/NumberOfSegments;x:=x1;A[1]:=x;A[2]:=f(x);
Repeat {konstrukce křivky jako lomené čáry}
B[1]:=x+hx;B[2]:=f(x+hx); Line(A,B,slBlue);A:=B;x:=x+hx
Until x>x2
end;
end;
Zde najdete kompletní zdrojový
kód a zde spustitelný kód
V případě
křivek bývá výhodné posloupnost bodů, kterými křivka prochází, nejdříve celou
spočítat a teprve potom proložit křivku.
Příklad 2: Předefinujme metodu PolyLine a funkci z př. 1. sestrojme pomocí této nové metody. Naše metoda bude pracovat s posloupností bodů, musíme tedy nejdříve deklarovat nový typ, nejlépe hned za TPoint:
TPoint = array [1..2] of Double;
TArrayOfPoints = array [0..800] of TPoint;
TPoint je tedy jeden bod - uspořádaná dvojice čísel, TArrayOfPoints je posloupnost nejvýše osmi set bodů. Do proměnné tohoto typu se budou ukládat body, kterými má procházet naše křivka. S nástroji, které již máme k dispozici, je její konstrukce jednoduchá:
procedure Draw2D.PolyLine(Q:TArrayOfPoints; n:Word;Color:Byte);
var
i:Word;
begin
MoveTo(Q[1]);
for
i:=1 to n do LineTo(Q[i],Color);
end;
Všimněme si nejdříve hlavičky: Q
je posloupnost bodů, n definuje počet bodů, které mají být spojeny, Color
pak barvu, kterou má být křivka sestrojena. Procedura nejdříve umístí pero do
prvního bodu pomocí naší metody MoveTo, do následujících pak kreslí úsečky naší
metodou LineTo. Samozřejmě je třeba upravit i naši proceduru
Explicit_Curve (uvádím pouze část kódu, která se od předchozího příkladu liší).
procedure TControl_Panel.Explicit_Curve(Sender:TObject);
var x,hx:Double; Q :TArrayOfPoints; i
:Word;
function f.....
begin
.......
hx:=(x2-x1)/NumberOfSegments;i:=0;x:=x1;
Repeat
Q[i,1]:=x;Q[i,2]:=f(x); {konstrukce křivky jako lomené čáry}
x:=x+hx;i:=succ(i);
Until x>x2+hx;
PolyLine(Q,i,Color);
end;
Zde najdete kompletní zdrojový
kód a zde spustitelný kód
Je zde jedna poněkud nepříjemná věc: V proměnné typu TArrayOfPoints nám přibyl jeden index, který udává pořadí bodu v posloupnosti. Ten je třeba uvádět vždy jako první. Zápis Q [i,2] tedy znamená, že se jedná o druhou souřadnici i - tého bodu v posloupnosti Q. Naši metodu PolyLine použijeme i při konstrukci křivek zadaných parametricky a polárně. Zde bude poněkud odlišný pouze způsob naplnění pole Q.
Z hlediska uživatele zůstává jiná nepříjemnost věc: z ovládacího panelu není možné měnit zadání funkce.
V příkladu 3, jehož zdrojový kód je zde a spustitelný kód je zde,
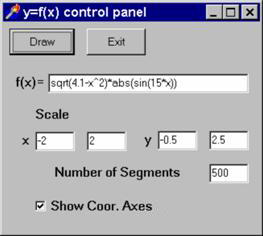
je tento nedostatek odstraněn. Řetezec zadávaný do okna EditFunction je vyčíslován v jednotce Graph2D_256 funkcí Calc(Text:String; ErrorReport:String). V zadávaném řetězci je možno zadávat všechny běžné funkce včetně cyklometrických, k označení proměnných lze použít x, y, t, k. ErrorReport vrací chybové hlášení. Máme-li k dispozici tuto proceduru, odpadá zadávání funkce f ve zdrojovém kódu. Proměnnou f deklarujeme jako řetězec a příkaz A[i,2]:=f(x) nahradíme příkazem A[i,2]:=Calc(f, ErrorReport). Řetězec ErrorReport je při korektním výpočtu správný. Při chybném vyhodnocení je vrácen popis chyby, čehož je možno využít k chybovému hlášení a přerušení procedury, např:
A[i,2]:=Calc(f, ErrorReport)
if ErrorReport<>’’
then begin
ShowMessage(ErrorReport);
exit;
end;
Samotné vyčíslení řetezce (funkce Calc) však není jednoduchou záležitostí, bezprostředně nesouvisí přímo s grafickými problémy a nebudeme se jím proto podrobněji zabývat.
Dříve, než postoupíme dále, je
třeba učinit ještě jednu poznámku. Barvy zadáváme v
procedure TControl_Panel.FormActivate(Sender:TObject);
begin
Draw2D.InitImage(Image1.Width,Image1.Height);
end;
procedure TControl_Panel.Explicit_Curve(Sender:TObject);
var x,hx:Double; Q :TArrayOfPoints; i
:Word;
function f.....
begin
.......
hx:=(x2-x1)/NumberOfSegments;i:=0;x:=x1;
Repeat
Q[i,1]:=x;Q[i,2]:=f(x); {konstrukce křivky jako lomené čáry}
x:=x+hx;i:=succ(i);
Until x>x2+hx;
PolyLine(Q,i,Color);
end;
Odkazy na kódy pracující v True Color režimu budeme uvádět takto:
True Color: zdrojový kód spustitelný kód
Křivky
zadané parametricky a polárně
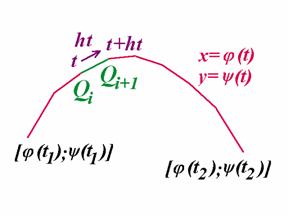
Konstrukce těchto křivek je velmi podobná, ukážeme si ji na konkrétním příkladu:
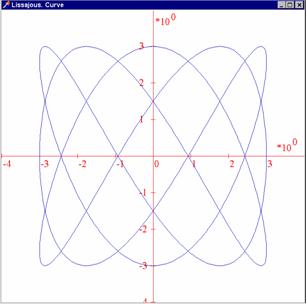
Příklad 1: Sestrojte křivku určenou
obecně parametrickými rovnicemi ![]() ;
; ![]() (jedná se o
tzv. Lissajousovy křivky, které opisuje kyvadlo rozkmitané ve dvou navzájem
kolmých rovinách a amplitudami
(jedná se o
tzv. Lissajousovy křivky, které opisuje kyvadlo rozkmitané ve dvou navzájem
kolmých rovinách a amplitudami ![]() ,
, ![]() a úhlovými
frekvencemi
a úhlovými
frekvencemi ![]() ;
;![]() ). Náš úkol řeší procedura Param_Curve. Nejprve jsou
deklarovány konstanty t1, t2, které definují rozsah parametru. Místo proměnných
x, hx je deklarován parametr t a jeho krok ht. Na deklaraci parametrických rovnic
ve zdrojovém kódu musíme místo funkce použít proceduru, neboť jako výstup
potřebujeme dvě proměnné - x, y.
). Náš úkol řeší procedura Param_Curve. Nejprve jsou
deklarovány konstanty t1, t2, které definují rozsah parametru. Místo proměnných
x, hx je deklarován parametr t a jeho krok ht. Na deklaraci parametrických rovnic
ve zdrojovém kódu musíme místo funkce použít proceduru, neboť jako výstup
potřebujeme dvě proměnné - x, y.
procedure TControl_Panel.Param_Curve (Sender:
TObject);
var i:Word;
procedure Lissajous(t:double;var x,y:double);
begin
x:=3*sin(3*t); y:=3*cos(5*t);
end;
begin
With Draw2D do
begin
ClearImage(slWhite); {vyplnění plochy bílou barvou}
Scale(x1,x2,y1,y2);
ht:=(t2-t1)/NumberOfSegments;
t:=t1;i:=0;
Repeat
Lissajous(t,Q[i,1],Q[i,2]);
t:=t+ht;i:=succ(i);
Until t>t2+ht;
PolyLine(Q,i,slBlue);
end;
end;
Výstupní parametry od vstupních je třeba v hlavičce procedury oddělit klíčovým slovem var. Následují parametrické rovnice (s konkrétními volbami za a, b, j, y). Ve vlastní proceduře jsem se omezil opět výhradně na konstrukci křivky. Nejdříve je potřeba nastavit krok parametru ht a jeho počáteční hodnotu. V cyklu pak naplňujeme pole Q parametrickými rovnicemi, dokud parametr t krokem ht neproběhne celý interval át1;t2ñ (indexem i počítáme body v posloupnosti Q). Nakonec křivku vykreslíme opět pomocí PolyLine.
Zde najdete kompletní zdrojový kód a zde spustitelný
kód
Příklad 2: opět poskytuje možnost měnit rovnici křivky za běhu programu.
Zde najdete kompletní zdrojový kód a zde spustitelný kód
True Color: zdrojový kód spustitelný kód
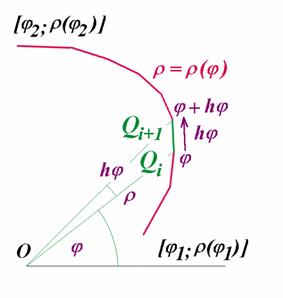
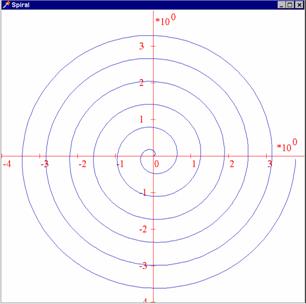
Příklad 3: Sestrojme křivku zadanou
v polárních souřadnicích. Postupujeme zcela analogicky. Základem je
procedura Polar_Curve,
kam zadáváme rovnici v polárních souřadnicích
a přepočet do souřadnic kartézských:
procedure TControl_Panel.Polar_Curve (Sender: TObject);
var i:Word;
procedure Spiral(fi:real;var x,y:real); var
rho:Real;
begin
rho:=0.1*fi; x:=rho*cos(fi); y:=rho*sin(fi);
end;
begin
With
Draw2D do
begin
Scale(x1,x2,y1,y2); fi:=fi1;i:=0;
hfi:=(fi2-fi1)/NumberOfSegments;
Repeat
Spiral(fi,Q[i,1],Q[i,2]);
fi:=fi+hfi;i:=succ(i);
Until
fi>fi2+hfi;
PolyLine(Q,i,slBlue);
end;
end;
Zde najdete kompletní zdrojový
kód a zde spustitelný kód
True Color: zdrojový
kód spustitelný kód
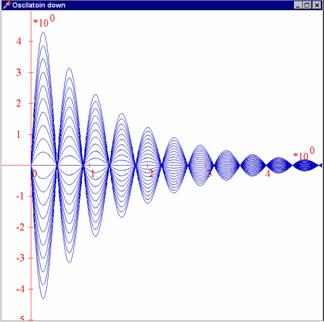
Příklad 4:
Je známo, že tlumené kmity jsou určeny rovnicí ![]() . Znázorněme tyto kmity za předpokladu, že
. Znázorněme tyto kmity za předpokladu, že ![]() . Příslušnou funkci nyní definujeme jako funkci dvou
proměnných:
. Příslušnou funkci nyní definujeme jako funkci dvou
proměnných:
function f(K,x:real):real;
begin f:=K*exp(-x)*sin(10*x); end;
Konstrukce systému křivek probíhá
nyní ve dvou do sebe vnořených cyklech: Ve vnějším probíhá ![]() krokem
krokem ![]() interval
interval ![]() , ve vnitřním pak
, ve vnitřním pak ![]() krokem
krokem ![]() interval
interval ![]() .
.
Najdete zde opět kompletní zdrojový kód i kompletní spustitelný kód.
True Color: zdrojový
kód spustitelný kód
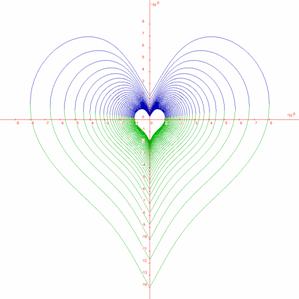
Příklad 5: Zajímavý parametrický systém funkcí získáme předpisem
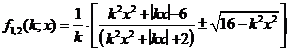 .
.
Na připojeném obrázku je
sestrojen pro ![]() krokem
krokem ![]() . Zeleně je sestrojen systém
. Zeleně je sestrojen systém ![]() (se znaménkem plus
před odmocninou), modře pak systém
(se znaménkem plus
před odmocninou), modře pak systém ![]() (se znaménkem
mínus).
(se znaménkem
mínus).
Příklad 6: Sestavme program, který
bude sestrojovat částečné součty funkčních řad - ![]() . Program se příliš neliší od př. 5. Místo výrazů
. Program se příliš neliší od př. 5. Místo výrazů ![]() vyčíslujeme výrazy
vyčíslujeme výrazy ![]() a neustále je
přičítáme. Tento příklad si však přesto zaslouží několik poznámek. Především má
uživatel opět možnost příslušnou řadu zadávat z ovládacího panelu: Zadaný
výraz je opět vyčíslován procedurou Calc.
a neustále je
přičítáme. Tento příklad si však přesto zaslouží několik poznámek. Především má
uživatel opět možnost příslušnou řadu zadávat z ovládacího panelu: Zadaný
výraz je opět vyčíslován procedurou Calc.
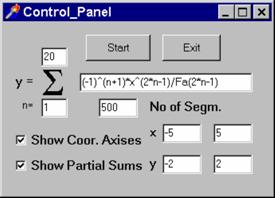
Aby tato procedura byla
použitelná na Taylorovy řady, je do ní zařazena funkce Fa, která počítá
faltoriál z celočíselného nezáporného argumentu. Zobrazený panel je připraven
na sestrojení prvních dvaceti částečných součtů Taylorovy řady funkce sinus:
![]() .
.
Dále je třeba zřejmě jednotlivé částečné
součty od sebe barevně odlišit. To lze zajistit mnoha
způsoby. V případě námi používaných osmibitových barev je možné nastavit
počáteční barvu na jedničku a po každé křivce
toto číslo o jedničku zvýšit.
Konstrukce funkčních řad si zaslouží poznámku. Výběr barev byl v osmibitových barvách jednoduchý - stačilo postupovat podle jejich pořadí. Zde je třeba si barvy i jejich pořadí nadefinovat. Definujeme celkem pět barev, které se pravidelně střídají, a udává číslo křivky a tím i barvy (je využito funkce mod, která vrací hodnoty zbytku po celočíselném dělení):
Procedure Colors;
var Modulo:Byte;
begin
Modulo:= n mod 5;
With Draw2D do
Case Modulo of
0:begin
Red:= 0;Green:= 0;Blue:=150;end;
1:begin Red:= 0;Green:=150;Blue:= 0;end;
2:begin
Red:=150;Green:= 0;Blue:= 0;end;
3:begin
Red:=120;Green:= 0;Blue:= 50;end;
4:begin Red:= 50;Green:= 0;Blue:=120;end;
end;
end;
Ovládací panel je oproti připojenému obrázku v řešeném příkladu vylepšen tak, že pro zadávání řad jsou k dispozici dva boxy - jeden pro řady Taylorovy, jeden pro Fourierovy. Poslední poznámka se týká připojených výstupů z tohoto příkladu: Je zde zobrazeno prvních 100 částečných součtů Taylorovy řady
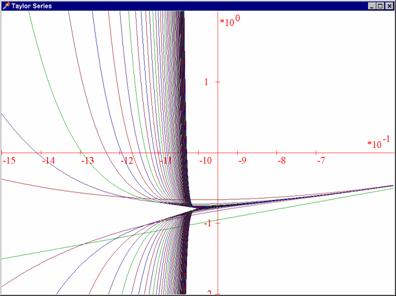
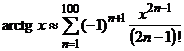
na hranici oboru konvergence a prvních deset částečných součtů Fourierovy řady
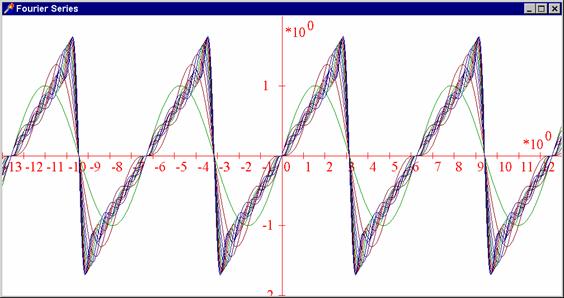
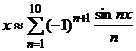
Zde najdete kompletní zdrojový kód a zde spustitelný kód
True Color: zdrojový kód spustitelný kód
Křivky
zadané rovnicí ![]()
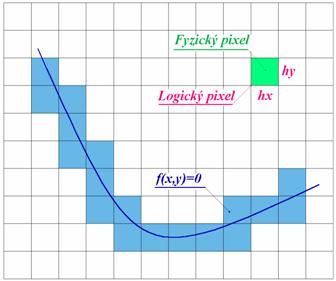
Nejjednodušší algoritmus pro
sestrojování těchto křivek využívá rozdílu mezi fyzickými
a logickými pixely (viz kpt. 2.1.). Křivku ![]() je možno vykreslit
samozřejmě pouze fyzickými pixely (viz světle modrá „křivka“ na přiložené
zvětšenině). Každý takový pixel je však logicky obdélník o stranách
je možno vykreslit
samozřejmě pouze fyzickými pixely (viz světle modrá „křivka“ na přiložené
zvětšenině). Každý takový pixel je však logicky obdélník o stranách ![]() (reálná velikost stran
závisí na rozměrech uživatelské kreslicí plochy). Je zřejmé, že fyzický pixel
má být vykreslen právě tehdy, protíná-li křivka hranice tohoto pixelu. Je tedy
třeba nastavit kroky
(reálná velikost stran
závisí na rozměrech uživatelské kreslicí plochy). Je zřejmé, že fyzický pixel
má být vykreslen právě tehdy, protíná-li křivka hranice tohoto pixelu. Je tedy
třeba nastavit kroky ![]()
![]() tak, aby „logické“ obdélníky
přesně pokrývaly „fyzické“ pixely. Kriteriem pro zobrazení fyzického pixelu
jsou pak různá znaménka funkce
tak, aby „logické“ obdélníky
přesně pokrývaly „fyzické“ pixely. Kriteriem pro zobrazení fyzického pixelu
jsou pak různá znaménka funkce ![]() alespoň ve dvou
vrcholech obdélníka. V algoritmu je tedy tedy nejdříve definovat funkci
alespoň ve dvou
vrcholech obdélníka. V algoritmu je tedy tedy nejdříve definovat funkci ![]() , výpis vlastního
algoritmu následuje.
, výpis vlastního
algoritmu následuje.
function f(x,y:double):double; {definována kružnice x2+y2-16=0}
begin f:=x*x+y*y-16; end;
begin
hx:=(x2-x1)/Image1.Width;
hy:=(y2-y1)/Image1.Height;
x:=x1;i:=0;
Repeat
y:=y1;
Repeat
if (f(x,y)*f(x,y+hy)<0) or
(f(x,y+hy)*f(x+hx,y+hy)<0)
then
begin A[1]:=x;A[2]:=y;PutPoint(A,slBlue); end;
y:=y+hy;
Until
y>y2;
x:=x+hx;i:=succ(i);
until x>x2;
end;
Příklad 1: V tomto příkladu jsou sestrojeny grafy křivek
x(x2+y2)-2(x2-y2)=0
x((x+1)2+y2)-2(x+1)2=0
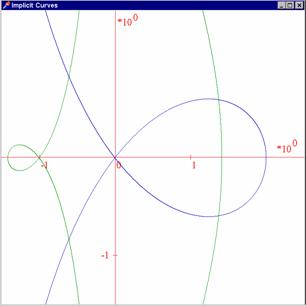
Zde najdete kompletní zdrojový
kód a zde spustitelný kód
Příklad 2 je opět doplněn o možnost zadávat rovnice za běhu programu z ovládacího panelu.
Zde najdete
kompletní zdrojový kód a zde spustitelný kód
True Color: zdrojový
kód spustitelný kód
Podobně jako jsme v předcházející kapitole sestrojovali systémy funkcí Kf(x), můžeme nyní sestrojovat systémy f(x,y)=K, což jsou vlastně vrstevnice plochy z= f(x,y). Přibývá zde opět cyklus pro parametr K.
Příklad 3:
Sestrojte vrstevnice plochy 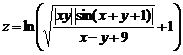
V tomto řešeném příkladu je voleno celkem 40 vrstevnic.
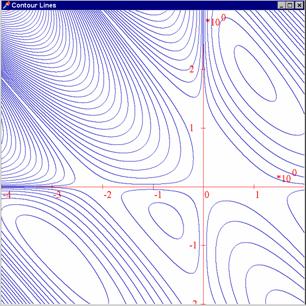
Zde najdete kompletní zdrojový
kód a
zde spustitelný kód
V příkladu 4 je předchozí příklad upraven tak, že uživatel má možnost volit rovnici, kreslicí plochu, interval parametru a počet křivek na panelu. Podmínku
if (f(x,y)*f(x,y+hy)<0) or (f(x,y+hy)*f(x+hx,y+hy)<0)
(viz fragment kódu před př. 1) je třeba nahradit voláním funkce Calc, např.
h1:=Calc(f,ErrorReport);y:=y+hy;
h2:=Calc(f,ErrorReport);x:=x+hx;
h3:=Calc(f,ErrorReport);x:=x-hx;y:=y-hy;
if (h1*h2<0) or (h2*h3<0) then...
(předpokládáme, že f je
vyhodnocovaný řetězec a h1,h2,h3 jsou proměnné deklarované jakou double).
Výhoda měnit rovnici křivky za běhu programu je ovšem zaplacena zpomalením výpočtu. Je to dáno tím, že procházíme statisíce (někdy i miliony bodů a v každém z nich třikrát voláme funkci Calc. Ta musí vyhodnocovaný řetězec vždy kompletně zpracovat, i když se předpis v cyklu vůbec nemění a je do něj potřeba pouze dosazovat různé hodnoty. Celý proces lze značně urychlit tím, že si řetězec před cyklem „předzpracujeme” funkcí PreCalc a v cyklu pak již pouze dosazujeme pomocí funkce PostCalc. Obě funkce jsou opět součástí knihovny Graph2D. Funkce Precalc(f:String;var ErrorReport):TExpression předzpracuje řetězec f a vrátí chybové hlášení (v případě chyby) a předzpracovaný výraz, který je možno uložit do proměnné Expression, která je deklarována opět v Graph2D. Funkce PostCalc pak proměnnou Expression vyhodnotí pro různé hodnoty proměnných. Příslušný fragment kódu pak vypadá takto:
Expression:=PreCalc(f,ErrorReport);
if ErrorReport<>’’ then begin ShowMessage(ErrorReport);Exit;end;
Repeat
y:=y1;
Repeat
h1:=PostCalc(Expression,ErrorReport);y:=y+hy;
if ErrorReport<>’’ then begin ShowMessage(ErrorReport);Exit;end;
h2:=PostCalc(Expression,ErrorReport);x:=x+hx;
if ErrorReport<>’’ then begin ShowMessage(ErrorReport);Exit;end;
h3:=PostCalc(Expression,ErrorReport);x:=x-hx;y:=y-hy;
if ErrorReport<>’’ then begin ShowMessage(ErrorReport);Exit;end;
if (h1*h2)<0) or (h2*h3)<0) then
begin A[1]:=x;A[2]:=y;PutPoint(A,slBlue); end;
y:=y+hy;
Until y>y2;
x:=x+hx;i:=succ(i);
until x>x2;
Kompletní kód zpracovaný pro True Color:
zdrojový
kód a
zde spustitelný kód
Síťová konstrukce: Výše uvedený
algoritmus je sice poměrně jednoduchý a nejpřesnější, jakého lze na daném
výstupním zařízení dosáhnout, jeho rychlost je však přes uvedené urychlení
mnohdy nedostatečná. Konstrukci lze urychlit za cenu poněkud menší přesnosti
následujícím způsobem: Na kreslicí plochu „položíme“ čtvercovou síť, přitom
strana čtverce je celočíselným násobkem strany fyzického pixelu (ve světových
souřadnicích je to tedy čtvercová síť, v uživatelských to však obecně jsou
obdélníky o stranách hx, hy, neboť uživatel může mít procedurou Scale
nastaveny na osách různé jednotky). Kreslicí plochu nyní nebudeme procházet bod
po bodu, ale po těchto obdélnících. Testováním znamének funkce ![]() ve vrcholech obdélníka
budeme zjišťovat, zda křivka protíná jeho obvod. Najdeme-li dvě takové strany,
pak metodou půlení intervalu zjistíme průsečíky A B s obvodem
s přesností na jeden fyzický pixel. Těmito body pak proložíme úsečku, čímž
vlastně křivku v tomto čtverci interpolujeme. Při realizaci programu
musíme rozlišit, zda půlíme svislou či vodorovnou stranu obdélníka. Uveďme
příklad „vodorovného“ půlení:
ve vrcholech obdélníka
budeme zjišťovat, zda křivka protíná jeho obvod. Najdeme-li dvě takové strany,
pak metodou půlení intervalu zjistíme průsečíky A B s obvodem
s přesností na jeden fyzický pixel. Těmito body pak proložíme úsečku, čímž
vlastně křivku v tomto čtverci interpolujeme. Při realizaci programu
musíme rozlišit, zda půlíme svislou či vodorovnou stranu obdélníka. Uveďme
příklad „vodorovného“ půlení:
Procedure HorizHalf(x1,x2,y:Double; var x:Double);
{vstupní parametry
v hlavičce mají stejný význam, jako při konstrukci osy x, výstupní
parametr udává x- ovou souřadnici nalezeného průsečíku.}
var i :Integer;
a,b,c:Double;
begin
a:=x1;b:=x2;
For i:=1 to Trunc(Step) do
begin {půlení intervalu a výběr intervalu s průsečíkem}
c:=(a+b)/2;if f(a,y)*f(c,y)<0 then b:=c else a:=c;
end;
x:=c;
{nastavení výstupní hodnoty}
end;
Dále je třeba zjistit, jak (a zda
vůbec) křivka testovaný čtverec protíná. Křivka ![]() protíná testovaný
čtverec zřejmě tehdy, když v jeho
vrcholech má funkce
protíná testovaný
čtverec zřejmě tehdy, když v jeho
vrcholech má funkce ![]() různá znaménka.
Ohodnoťme vrcholy čtverce
různá znaménka.
Ohodnoťme vrcholy čtverce ![]() postupně hodnotami
postupně hodnotami ![]() ;
; ![]() ;
; ![]() ;
; ![]() , a to právě tehdy, když v příslušném vrcholu je
, a to právě tehdy, když v příslušném vrcholu je ![]() , jinak vrcholu přiřaďme nulu. Celý čtverec tak může být
ohodnocen hodnotami
, jinak vrcholu přiřaďme nulu. Celý čtverec tak může být
ohodnocen hodnotami ![]() - z hlediska naší
konstrukce existuje právě šestnáct způsobů, jak může sestrojovaná křivka
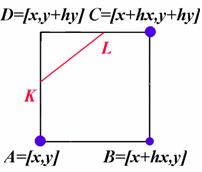
testovaný čtverec protínat. Čtverec na obrázku vlevo je ohodnocen číslem
- z hlediska naší
konstrukce existuje právě šestnáct způsobů, jak může sestrojovaná křivka
testovaný čtverec protínat. Čtverec na obrázku vlevo je ohodnocen číslem ![]() , čtverec vpravo pak číslem
, čtverec vpravo pak číslem ![]() . Součet těchto ohodnocení je
. Součet těchto ohodnocení je ![]() a je zřejmé, že postup
konstrukce bude v obou případech stejný - v obou případech je třeba hledat
průsečíky na úsečkách
a je zřejmé, že postup
konstrukce bude v obou případech stejný - v obou případech je třeba hledat
průsečíky na úsečkách ![]() ,
, ![]() . Ačkoli je tedy celkový počet případů, které je třeba řešit,
čtrnáct (čtverce s ohodnoceními 0 resp.15 křivka neprotíná), program stačí
větvit pouze na sedm větví. Zajímavé vyjádření ohodnocení je ve dvojkové
soustavě, kdy bod je ohodnocen pouze nulou, či jedničkou. Např. pro levý
obrázek máme:
. Ačkoli je tedy celkový počet případů, které je třeba řešit,
čtrnáct (čtverce s ohodnoceními 0 resp.15 křivka neprotíná), program stačí
větvit pouze na sedm větví. Zajímavé vyjádření ohodnocení je ve dvojkové
soustavě, kdy bod je ohodnocen pouze nulou, či jedničkou. Např. pro levý
obrázek máme:
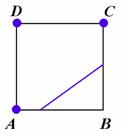
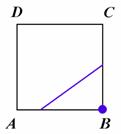
![]()
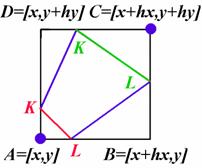
Konečně je třeba si uvědomit, že
v případě ![]() resp.
resp. ![]() nelze jednoznačně
rozhodnout, jak interpolační úsečky vlastně sestrojit (viz možnosti 5, 10 v
připojené sekvenci kódu - obrázek na další straně). V tom případě je třeba
vybrat jen jednu z obou možností.
nelze jednoznačně
rozhodnout, jak interpolační úsečky vlastně sestrojit (viz možnosti 5, 10 v
připojené sekvenci kódu - obrázek na další straně). V tom případě je třeba
vybrat jen jednu z obou možností.
begin
hx:=Step*(x2-x1)/Image1.Width; {po obvyklém přečtení hodnot
z Control}
hy:=Step*(y2-y1)/Image1.Height; {Panelu a nastavení
měřítka nastavíme }
x:=x1; {kroky hx, hy tak,aby přesně odpovídaly uživatelským
rozměrům}
Repeat {fyzického pixelu
a začínáme procházet síť}
y:=y1; {Proměnná
h bude určovat, na kterých}
Repeat {stranách čtverce
byly nalezeny průsečíky}
h:=0;
if f(x,y) >0 then h:=h+8;
if f(x+hx,y) >0 then h:=h+4;
if f(x+hx,y+hy)>0 then
h:=h+2;
if f(x ,y+hy)>0 then h:=h+1;
Case
h of
1,14:begin
K[1]:=x;VertHalf(y,y+hy,x,K[2]);
HorizHalf(x,x+hx,y+hy,L[1]);L[2]:=y+hy;
Line(K,L,Red,Green,Blue);
end;
5,10:begin
K[1]:=x ;VertHalf(y,y+hy,x+hx,K[2]);
HorizHalf(x,x+hx,y,L[1]);L[2]:=y;
Line(K,L,Red,Green,Blue);
K[1]:=x ;VertHalf(y,y+hy,x,K[2]);
HorizHalf(x,x+hx,y+hy,L[1]);L[2]:=y+hy;
Line(K,L,Red,Green,Blue);
end;
……………………………………………………………….. {ostatní případy analogicky}
end;
y:=y+hy;
Until y>y2;
x:=x+hx;
until x>x2;
V příkladu 5 je předchozí algoritmus zpracován.
Zde najdete kompletní zdrojový
kód a
zde spustitelný
kód
Podobným způsobem lze konstruovat
plochy určené rovnicí ![]() v prostoru. Zde se
podobným způsoben hledají průsečíky plochy s hranami krychle a plocha se
interpoluje pomocí trojúhelníků. Různých možností však není čtrnáct resp. sedm,
ale 254 resp. 127. Tímto problémem se budeme zabývat dále
v prostoru. Zde se
podobným způsoben hledají průsečíky plochy s hranami krychle a plocha se
interpoluje pomocí trojúhelníků. Různých možností však není čtrnáct resp. sedm,
ale 254 resp. 127. Tímto problémem se budeme zabývat dále