Interpolace
Interpolační
polynom
Jedná se o polynom ![]() stupně, který má
procházet n zadanými body. Tento problém lze řešit tzv. metodou neurčitých
koeficientů: Polynom
stupně, který má
procházet n zadanými body. Tento problém lze řešit tzv. metodou neurčitých
koeficientů: Polynom ![]() stupně má obecně
rovnici
stupně má obecně
rovnici
![]()
Dosadíme-li do této rovnice
postupně všechny body ![]() , kterými má polynom procházet, dostaneme pro neznámé
koeficienty
, kterými má polynom procházet, dostaneme pro neznámé
koeficienty ![]() soustavu lineárních
rovnic
soustavu lineárních
rovnic
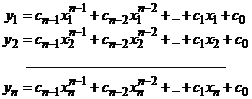 (1)
(1)
Řešením této soustavy dostáváme neznámé koeficienty a tím i hledaný polynom
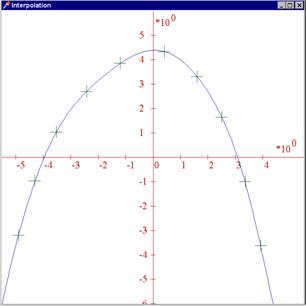
Příklad 1: Zde najdete zprogramované hledání interpolačního polynomu metodou neurčitých koeficientů (výstup viz přiložený obrázek).
Obrázek na následující straně dobře ilustruje známou nepříjemnou vlastnost interpolačního polynomu, že totiž sice prochází zadanými body, mezi nimi se však může chovat velmi divoce. Metoda neurčitých koeficientů je však značně nevhodná, a to zvláště tehdy, je-ji počet uzlových bodů větší a soustava (1) řešena Gaussovou eliminací. Je totiž velmi špatně podmíněna a výsledky jsou značně nejisté.
Zde najdeme kompletní zdrojový kód a zde spustitelný kód
True Color: zdrojový kód spustitelný kód
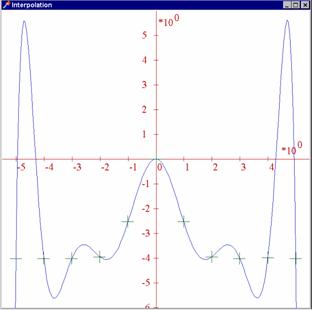
Příklad 2:
Najděme interpolační polynom
Lagrangeovou metodou. Lagrange odvodil, že polynom procházející body ![]() je
je
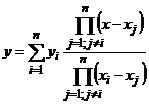
Tento vzorec je vyčíslován funkcí Lagrange:
Function Lagrange(z:Double):Double
var i,j
:Integer;
Lagr,Citatel,Jmenovatel:Double;
begin
Lagr:=0;
for
i:=1 to n do
begin
Citatel:=1;Jmenovatel:=1;
for j:=1 to n do
if
i<>j then
begin
Citatel:=Citatel*(z-x[j]);
Jmenovatel:=Jmenovatel*(x[i]-x[j]);
end;
Lagr:=Lagr+y[i]*Citatel/Jmenovatel;
end;
Lagrange:=Lagr;
end;
Tento algoritmus je numericky
stabilní, stručnější a velmi spolehlivý. Proměnná funkce je (na rozdíl od
vzorce) označena z. Je to proto, že v programu nemůžeme používat označení
x a x[i] pro dvě různé proměnné.
Zde najdeme kompletní zdrojový kód a zde spustitelný kód
True Color: zdrojový
kód spustitelný kód
Kubický
splajn
Odvození rovnice kubického
splajnu zde nebudeme provádět. Zájemce ji může nalézt např. v [Maro]. Uveďme
jen výsledek. Připomeňme, že se jedná o křivku, která prochází všemi
zadanými body, na celém zadaném intervalu je spojitá i se svou 1. a 2.
derivací a na každém subintervalu určeném x-ovými souřadnicemi uzlových
bodů splývá s nějakou kubickou parabolou. Jsou-li ![]() uzlové body a
uzlové body a ![]() , pak na intervalu
, pak na intervalu![]() je rovnice splajnu
je rovnice splajnu
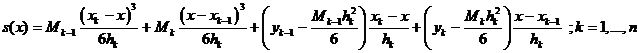 (1)
(1)
kde koeficienty ![]() můžeme volit
(většinou je pokládáme rovny nule) a
můžeme volit
(většinou je pokládáme rovny nule) a ![]() pro
pro
![]() dostaneme jako
řešení soustavy
dostaneme jako
řešení soustavy
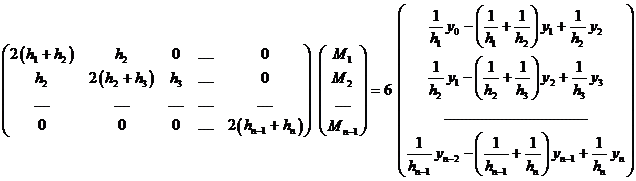
Tato soustava je ostře diagonálně
dominantní, proto ji s výhodou můžeme řešit iteračními metodami,
odvozovanými v numerické matematice.
Příklad 1.: Sestrojme kubický
splajn který prochází zadanými uzlovými body. Jádrem programu je procedura pro
řešení výše uvedené třídiagonální soustavy:
procedure
GaussSeidel;
var i,j:Integer;
begin
for i:=1 to n-1 do M[i]:=0;
for j:=1 to
CountOfIter do
begin
M[1]:=(1/h[1]*y[0]-(1/h[1]+1/h[2])*y[1]+1/h[2]*y[2]-
h[2]*M[2]/2/(h[1]+h[2]);
for i:=2 to n-2 do
M[i]:=(1/h[i-1]*y[i-2]-(1/h[i-1]+1/h[i])*y[i-1]
+1/h[i]*y[i]-(h[i]*M[i-1]+h[i+1]*M[i+1])/2/(h[i]+h[i+1]);
M[n-1]:=(1/h[n-1]*y[n-2]-(1/h[n-1]+1/h[n])*y[n-1]
+1/h[n]*y[n]-h[n-1]*M[n-2])/2/(h[n-1]+h[n]);
end;
end;
Dále je třeba Function Spline(k:Integer;x:Double):Double; která počítá
funkční hodnotu splajnu pro dané ![]() . Obsahuje pouze přepsaný vzorec (1), a proto ji
zde nebudu uvádět. Vlastní vykreslení provádí procedura Construct:
. Obsahuje pouze přepsaný vzorec (1), a proto ji
zde nebudu uvádět. Vlastní vykreslení provádí procedura Construct:
Procedure Construct;
var i,j:integer;hx:Double;A:TArrayOfPoints;
begin
for i:=1 to n do
begin
hx:=(x[i]-x[i-1])/20;
for
j:=1 to 20 do
begin
A[i,1]:=x[i-1]+(i-1)*hx;A[i,2]:=Spline(j,A[i,1]);
end;
PolyLine(A,20,slBlue);
end;
end;
Zde najdeme kompletní zdrojový kód a zde spustitelný kód
True Color: zdrojový kód spustitelný kód
Z výstupu z tohoto
programu je patrné, že kubický splajn již netrpí nedostatky Lagrangeova
polynomu. V technické praxi
i v CAD systémech je hojně používán. Analogické použití mají tzv. B -
splajny, o kterých pojednáme dále.
Aproximační křivky
Polynom
metodou nejmenších čtverců
V technické praxi stojíme často
před problémem nalézt křivku, která neprochází přesně zadanými body, ale
vystihuje závislost dvou veličin, jejichž hodnoty získáme měřením. Tyto křivky
získáváme tzv. metodou nejmenších čtverců a nejčastěji je hledáme ve tvaru
polynomu. Aproximujme ![]() naměřených hodnot
naměřených hodnot ![]() polynomem
polynomem ![]() -tého stupně
-tého stupně ![]() . Neznámé koeficienty
. Neznámé koeficienty ![]() dostaneme řešením
soustavy
dostaneme řešením
soustavy
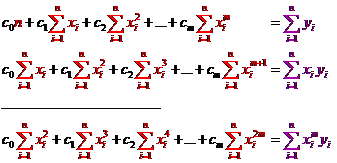
Řešením této soustavy dostáváme
pak neznámé koeficienty ![]() a tím neznámý polynom.
a tím neznámý polynom.
Příklad 1: Naprogramujme proložení polynomu zadanými hodnotami metodou nejmenších čtverců.
Programové zpracování musíme pak
rozdělit do několika částí: především naprogramujeme výpočet mocniny ![]() , který se velmi často opakuje:
, který se velmi často opakuje:
Function Power(Basis:Double;Exponent:Integer):Extended;
var Pow:Extended;
i:Integer;
begin
Pow:=1;
if abs(Exponent)>0 then for i:=1 to Abs(Exponent) do
Pow:=Pow*Basis;
if Exponent<0 then Pow:=1/Pow;
Power:=Pow;
end;
Následuje generování soustavy:
Procedure GenerOfSystem;
var i,j,k:Integer; {indexy}
x,y:array [1..100] of Extended; {pole pro naměřené hodnoty}
begin
for k:=1 to index do {naplnění "naměřených" hodnot uživatelem zadanými body}
begin
x[k]:=P[k,1];y[k]:=P[k,2];end;
{nulování
koeficientů soustavy}
for i:=0 to n do for j:=0 to n do a[i,j]:=0;
for i:=0 to n do b[i]:=0;
for i:=0 to n do
begin
for
j:=0 to n do for k:=1 to index do
a[n-i,n-j]:=a[n-i,n-j]+Power(x[k],i+j);
{vzhledem k tomu, že soustava je většinou
špatně podmíněná a že bude řešena
Gaussovou eliminací, je matice soustavy "překlopena"
podle vedlejší diagonály - a[n-i,n-j] místo
a[i,j] a sloupec pravých stran
zadáván v opačném pořadí - b[n-i]
místo b[i]}
for
k:=1 to index do b[n-i]:=b[n-i]+y[k]*Power(x[k],i);end;
end;
Takto vygenerovaná soustava je
řešena Gaussovou eliminací a získaný polynom vykreslován procedurou
AproxCurve:
procedure AproxCurve;
const
NoOfSegments=100;
var Q:TArrayOfPoints;
begin
With Draw2D do
begin
Q[0,1]:=x1;hx:=(x2-x1)/NoOfSegments;
for
i:=1 to NoOfSegments do Q[i,1]:=Q[i-1,1]+hx;
for
i:=0 to NoOfSegments do Q[i,2]:=0;
for
i:=0 to NoOfSegments do
for j:=0 to n do
Q[i,2]:=Q[i,2]+c[n-j]*Power(Q[i,1],j);
PolyLine(Q, NoOfSegments,slBlue);
end;
end;
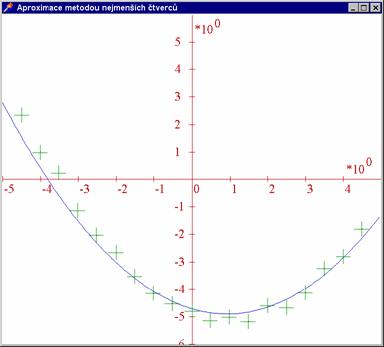
Zde najdeme kompletní zdrojový kód a zde spustitelný kód
True Color: zdrojový
kód spustitelný kód
Fergusonovy
křivky
Doposud jsme se zabývali křivkami
určenými analyticky (tj. rovnicí), nebo tabulkovými hodnotami, ať již přesnými
(interpolace), nebo zatíženými vstupními chybami (aproximace metodou nejmenších
čtverců). V ideálním případě (pokud by neexistovaly chyby měření) by
i v tomto případě křivka body procházela. Technická praxe často
vyžaduje křivky, určené body, kterými křivka nemusí procházet a jejichž
poloha určuje křivku jiným způsobem. Hovoříme o řídících bodech nebo o
řídícím polygonu. Jednu z nejjednodušších takových křivek používal od r.
1964 J. C. Ferguson. (viz přiložený obrázek). Křivka je určena dvěma
krajními body ![]() ,
, ![]() a dvěma
tečnými vektory
a dvěma
tečnými vektory ![]() ,
, ![]() . Velikost těchto vektorů ovlivňuje zároveň
druhou derivaci křivky (čím je velikost větší, tím více křivka k vektoru „přimyká“).
Křivka je definována parametrickými rovnicemi
. Velikost těchto vektorů ovlivňuje zároveň
druhou derivaci křivky (čím je velikost větší, tím více křivka k vektoru „přimyká“).
Křivka je definována parametrickými rovnicemi
![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]()
Funkce ![]() jsou polynomy 3. stupně,
Fergusonova křivka je tedy kubická parabola.
jsou polynomy 3. stupně,
Fergusonova křivka je tedy kubická parabola.
Příklad 1: Programové zpracování
Fergusonovy křivky. Při něm pouze rozepíšeme
výše uvedené vztahy do dvou souřadnic:
Procedure
Ferguson(t:Double; var Q:TPoint);
begin
Q[1]:=P[0,1]*(2*t*t*t-3*t*t+1)+P[1,1]*
(-2*t*t*t+3*t*t)+P[2,1]*(t*t*t-2*t*t+t)+P[3,1]*(t*t*t-t*t);
Q[2]:=P[0,2]*(2*t*t*t-3*t*t+1)+P[1,2]*
(-2*t*t*t+3*t*t)+P[2,2]*(t*t*t-2*t*t+t)+P[3,2]*(t*t*t-t*t);
end;
Výstupy z této procedury postupně naplníme proměnnou typu TArrayOfPoints
a křivku pak jednoduše zobrazíme procedurou PolyLine (řešeno
v osmibitové batevné hloubce):
begin
x1:=5;x2:=300;y1:=10;y2:=300;
Scale(x1,x2,y1,y2);
{řídící
body - v řešeném příkadu zadávané myší}
P[0,1]:= 10;P[0,2]:= 10;P[1,1]:= 30;P[1,2]:=150;
P[2,1]:= 90;P[2,2]:=250;P[3,1]:=140;P[3,2]:=170;
Line(P[0],P[1],slRed);Line(P[2],P[3],slRed); {kresba řídících vektorů}
ht:=0.01;t:=0;i:=0; {generace Fergusonovy křivky}
While t<1 do begin
Ferguson(t,Q[i]);i:=succ(i);t:=t+ht;end;
PolyLine(Q,i-1,slGreen); {konstrukce
Fergusonovy křivky}
end;
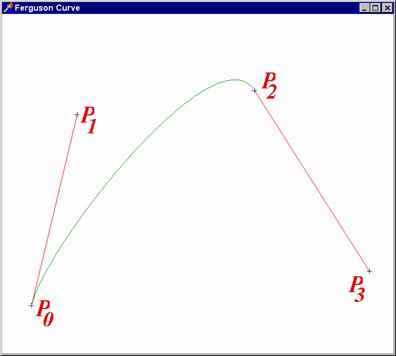
Zde najdeme kompletní zdrojový kód a zde spustitelný kód
True Color: zdrojový
kód spustitelný kód
Bézierovy
křivky
V letech 1959 - 1962 navrhli nezávisle na sobě
P. E. Béziere a P. de Casteljau křivku, která je určena čtyřmi body ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Je definována parametrickými rovnicemi
. Je definována parametrickými rovnicemi
![]() ;
;
![]() ;
;![]() ;
;![]() ;
;![]()
Příklad 1: Programové zpracování Bézierovy
křivky: Při programovém zpracování opět pouze rozepíšeme výše uvedené vztahy do
dvou souřadnic:
Procedure Beziere(t:Double;var
Q:TPoint);
begin
Q[1]:=P[0,1]*(1-t)*(1-t)*(1-t)+P[1,1]*3*t*(1-t)*
(1-t)+P[2,1]*3*t*t*(1-t)+P[3,1]*t*t*t;
Q[2]:=P[0,2]*(1-t)*(1-t)*(1-t)+P[1,2]*3*t*(1-t)*
(1-t)+P[2,2]*3*t*t*(1-t)+P[3,2]*t*t*t;
end;
Výstupy z této procedury stejně jako v předchozím případě
postupně naplníme proměnnou typu TArrayOfPoints a křivku pak jednoduše
zobrazíme procedurou PolyLine (řešeno v osmibitové batevné hloubce):
begin
x1:=5;x2:=300;y1:=10;y2:=300;Scale(x1,x2,y1,y2);
{řídící
body - v řešeném příkadu zadávané myší}
P[1,1]:= 10;P[1,2]:= 10;P[2,1]:=
30;P[2,2]:=150;
P[3,1]:= 90;P[3,2]:=250;P[4,1]:=140;P[4,2]:=170;
Line(P[1],P[2],slRed);Line(P[2],P[3],slRed);
Line(P[3],P[4],slRed);
ht:=0.01;t:=0;i:=1; {generace Béziérovy křivky}
While t<1 do
begin Beziere(t,C[i]);i:=succ(i);t:=t+ht;end;
PolyLine(C,i-1,0,slGreen); {konstrukce Béziérovy křivky}
end;
Jedná se o kubickou parabolu, která prochází
body ![]() ,
, ![]() , úsečky
, úsečky ![]() ,
, ![]() určují tečny
v krajních bodech a jejich směrnice jsou číselně rovny třetině délky
těchto úseček.
určují tečny
v krajních bodech a jejich směrnice jsou číselně rovny třetině délky
těchto úseček.
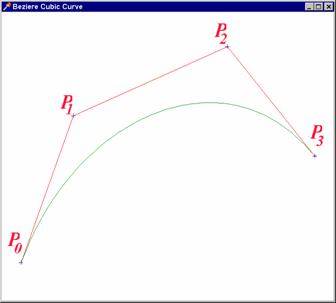
Zde najdeme kompletní zdrojový kód a zde spustitelný kód
True Color: zdrojový kód spustitelný kód
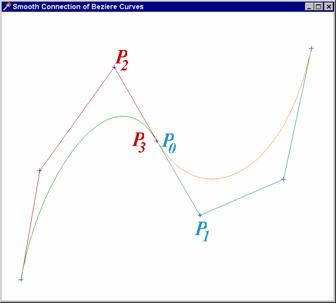
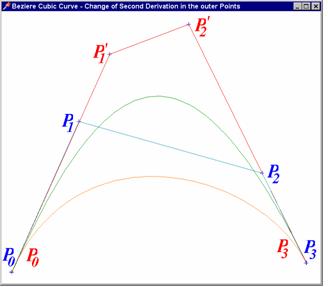
Výstup (upravený popisem) vidíte na prvním připojeném obrázku. Jedním z důvodů obliby těchto křivek v technické praxi je jejich snadné „hladké“ napojování. Ve spojovacím bodě lze totiž snadno docílit spojitosti křivky i její derivace - totiž tím, že v bodě spojení zajistíme společnou tečnu.
Příklad 2 ukazuje, jak toho
dosáhnout: Koncový bod ![]() jedné křivky je
pochopitelně totožný s počátkem
jedné křivky je
pochopitelně totožný s počátkem ![]() následující
křivky a bod
následující
křivky a bod ![]() „předchůdce“ je
středově souměrný s bodem
„předchůdce“ je
středově souměrný s bodem ![]() „následovníka“ podle
společného bodu
„následovníka“ podle
společného bodu ![]() . Takto vzniklá křivka má ve všech vnitřních bodech
spojitost prvního řádu.
. Takto vzniklá křivka má ve všech vnitřních bodech
spojitost prvního řádu.
Zde najdeme kompletní zdrojový kód a zde spustitelný kód
True Color: zdrojový kód spustitelný
kód
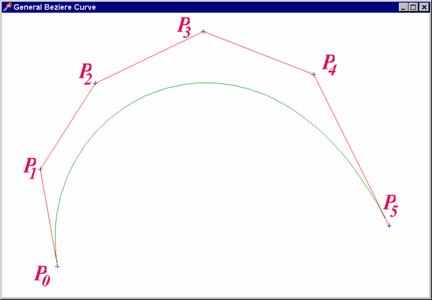
Příklad 3 - obecná Bézierova
křivka: vznikne zobecněním předchozího případu. Křivka ![]() tého stupně vznikne pomocí
tého stupně vznikne pomocí ![]() řídících bodů
a je určena vztahem
řídících bodů
a je určena vztahem
![]()
![]() jsou tzv. Bernsteinovy polynomy (pro
jsou tzv. Bernsteinovy polynomy (pro ![]() dostaneme předchozí
případ, na připojeném obrázku je
dostaneme předchozí
případ, na připojeném obrázku je ![]() ). V programovém zpracování přibývá výpočet faktoriálu
a kombinačního čísla
). V programovém zpracování přibývá výpočet faktoriálu
a kombinačního čísla ![]()
Function Factorial(n:Integer):LongInt;
var Fa,i:LongInt;
begin
Fa:=1;
if n>1 then for
i:=2 to n do Fa:=Fa*i;
Factorial:=Fa;
end;
Function
Combin(n,i:Integer):LongInt;
begin
Combin:=Trunc(Factorial(n)/Factorial(n-i)/Factorial(i));
end;
Function
Power(Basis:Real;Exponent:Integer):Extended;
var
Pow:Extended;
i: Integer;
begin
Pow:=1;
if abs(Exponent)>0 then
for i:=1 to Abs(Exponent) do Pow:=Pow*Basis;
if Exponent<0 then Pow:=1/Pow;
Power:=Pow;
end;
Function
Bernstein(n,i:Integer):Double;
begin
Bernstein:=Combin(n,i)*Power(t,i)*Power(1-t,n-i);
end;
Zde najdeme kompletní zdrojový kód a zde spustitelný kód
True Color: zdrojový kód spustitelný kód
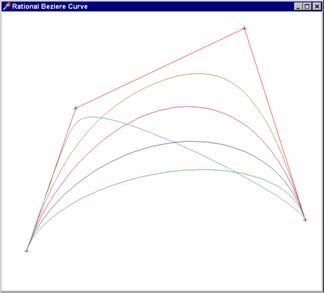
Příklad 4 - racionální Bezierova křivka: Předchozí příklady Bezierových křivek měly jednu společnou nevýhodu: řídícími body jsou určeny jednoznačně. Jinými slovy ke změně tvaru je potřeba změnit řídící body. To může být dosti nepříjemné, zvláště v případě, jestliže sice chceme měnit tvar křivky, nikoli však tečny v krajních bodech (v krajních bodech chceme měnit druhou derivaci, nikoli však první).
Chceme-li např. dle připojeného
obrázku více vyklenout původní oranžovou křivku určenou polygonem ![]() , je to s dosavadními křivkami možné pouze tak, že krajní řídící body zůstanou na místě
a novou polohu
, je to s dosavadními křivkami možné pouze tak, že krajní řídící body zůstanou na místě
a novou polohu ![]() resp
resp ![]() zvolíme tak, aby
ležely na původních tečnách
zvolíme tak, aby
ležely na původních tečnách ![]() , resp
, resp ![]() . To nebývá vždy jednoduché. Přirozenější
je poměrně jednoduché zobecnění, kdy každému řídícímu bodu
. To nebývá vždy jednoduché. Přirozenější
je poměrně jednoduché zobecnění, kdy každému řídícímu bodu ![]() přiřadíme nezáporné reálné číslo
přiřadíme nezáporné reálné číslo ![]() , které ovlivňuje tvar křivky. Ta má potom tvar:
, které ovlivňuje tvar křivky. Ta má potom tvar:
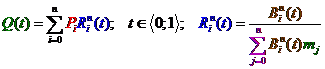
jsou tzv. racionální Bernsteinovy polynomy a ![]() jsou tyv. Bernsteinovy
polynomy.
jsou tyv. Bernsteinovy
polynomy.
begin
A[1]:=0;A[2]:=0;
for i:=0 to n do
begin
R[i]:=Bernstein(n,i)*m[i];Value:=0;
for j:=0 to n do
Value:=Value+Bernstein(n,j)*m[j];
A[1]:= A[1]+R[i]*P[i,1]/Value;
A[2]:= A[2]+R[i]*P[i,2]/Value;
end;
end;
Na připojeném obrázku je znázorněno
pět křivek se stejným řídícím polygonem. Pro všechny je ![]() , pro čtyři
z nich pak
, pro čtyři
z nich pak ![]() , a to
postupně 0,2; 0,4; 1; 4; u poslední je pak
, a to
postupně 0,2; 0,4; 1; 4; u poslední je pak ![]() .
.
Zde najdeme kompletní zdrojový kód a zde spustitelný kód
True Color: zdrojový kód spustitelný kód
Coonsovy
křivky a B-splajny
Další křivky hojně používané v technické praxi
definoval S. A. Coons. Coonsova kubika je definována opět čtyřmi řídícími body ![]() a kubickými polynomy
a kubickými polynomy ![]() :
:
![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]()
Příklad 1.: Programové zpracování
Coonsovy kubiky je zcela analogické jako u kubiky Bezierovy (funkční
předpis se liší pouze zlomkem a v předpisu pro dva „bázové“ polynomy).
Zde najdeme kompletní zdrojový kód a zde spustitelný kód
True Color: zdrojový
kód spustitelný kód
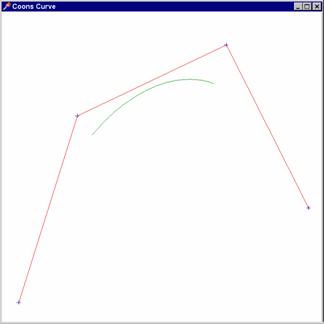
Výstup z programu vidíme na obrázku. Je patrné, že Coonsova kubika má
poněkud jiné vlastnosti než Béziérova. Především neprochází ani jedním
z řídících bodů (krajní body leží v tzv. antitěžištích ![]() ,
, ![]() ). Výhoda
Coonsových kubik vynikne nejlépe v okamžiku, kdy je použijeme ke skládání.
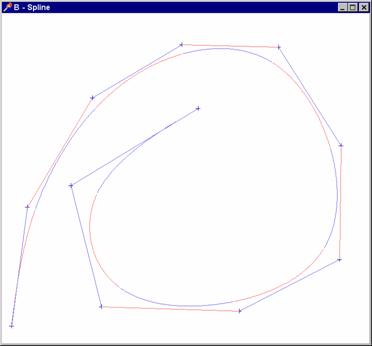
Coonsovy kubiky skládáme tak, že vždy dva sousední oblouky mají společné tři ze
čtyř řídících bodů. Dostáváme tak křivku nazývanou B-splajn, která je ve všech
vnitřních bodech spojitá i se svou první i druhou derivací -
spojitost druhého řádu (je „hladší“, než křivka Bézierova). Při „tvarování“
křivky je z technického hlediska výhodné také to, že při změně jednoho řídícího
bodu dochází pouze k lokální změně křivky (totiž pouze čtyř oblouků,
jejichž konstrukce se daný bod účastní). A ještě jednu poznámku: kubický
Coonsův oblouk sice neprochází ani jedním z řídících bodů,
u B splajnu však incidenci krajních bodů lze zajistit, a to tím,
že tři řídící body prvního resp. posledního oblouku splynou.
). Výhoda
Coonsových kubik vynikne nejlépe v okamžiku, kdy je použijeme ke skládání.
Coonsovy kubiky skládáme tak, že vždy dva sousední oblouky mají společné tři ze
čtyř řídících bodů. Dostáváme tak křivku nazývanou B-splajn, která je ve všech
vnitřních bodech spojitá i se svou první i druhou derivací -
spojitost druhého řádu (je „hladší“, než křivka Bézierova). Při „tvarování“
křivky je z technického hlediska výhodné také to, že při změně jednoho řídícího
bodu dochází pouze k lokální změně křivky (totiž pouze čtyř oblouků,
jejichž konstrukce se daný bod účastní). A ještě jednu poznámku: kubický
Coonsův oblouk sice neprochází ani jedním z řídících bodů,
u B splajnu však incidenci krajních bodů lze zajistit, a to tím,
že tři řídící body prvního resp. posledního oblouku splynou.
Příklad 2.: Programové zpracování B-splajnu: Protože
budeme chtít navazovat více Coonsových oblouků, Vyvedeme si je do samostatné
procedury:
Procedure
CoonsArc(Color:Byte);
begin
t:=0;i:=1;
While t<1 do begin
Coons(t,C[i]);i:=succ(i);t:=t+ht;end;
PolyLine(C,i-1,Color);
end;
begin
x1:=10;x2:=340;y1:=0;y2:=250; {měřítko a řídící
body}
Scale(x1,x2,y1,y2);ht:=0.01;
P[1,1]:=10;P[1,2]:= 10;P[2,1]:=
30;P[2,2]:=150;
P[3,1]:=90;P[3,2]:=250;P[4,1]:=140;P[4,2]:=
70;
CoonsArc(200,0,0); {první oblouk}
P[1]:=P[2];P[2]:=P[3];P[3]:=P[4]; {posun řídících
bodů}
P[4,1]:=150;P[4,2]:= 0;
CoonsArc(0,200,0); {druhý oblouk}
end;
Zde najdeme kompletní zdrojový kód a zde spustitelný kód
True Color: zdrojový
kód spustitelný
kód