Globální zobrazovací metody
Všechny dosud uvedené metody fungovaly za dosti přísných omezujících podmínek. Tělesa byla osvětlena pouze jedním zdrojem, zobrazovali jsme nanejvýše dvě tělesa, která se navzájem neovlivňovala buď vůbec, nebo se ovlivňovala velmi málo - např. stín vržený na podložku, průhledná plocha či těleso nad vodorovnou rovinou. Často je však třeba zobrazovat více těles z různých materiálů osvětlených několika světelnými zdroji s různými vlastnostmi, což má za následek vznik nejrůznějších optických jevů. K postižení těchto jevů je třeba použít metody, které neřeší jen jeden optický jev (tedy např. jen zastínění tělesa či lom na rozhraní dvou prostředí), ale metody, které se snaží postihnout co nejvíce vzájemných optických vztahů mezi jednotlivými předměty, které se ve zobrazovaném prostoru - scéně nacházejí. Tyto metody se nazývají globální zobrazovací metody.
Rastrové texturování kulové plochy
Globální zobrazovací metody jsou většinou náročné z hlediska počtu potřebných operací. Proto se při nich ve speciálních případech používají také speciální metody, které jsou rychlejší než metody obecné. Velmi často je třeba vyhodnotit chvání světla na povrchu koule. V následujících kapitolách se tedy budeme zabývat odrazem a lomem světla na tomto povrchu, v této kapitole si všimneme efektivních metod používaných speciálně na texturování kulové plochy.
Víme již, že aplikaci textury na
povrch tělesa provedeme definováním tzv. mapovací funkce 
, která každému bodu z definičního oboru textury přiřadí
bod 
na povrchu 
tělesa. Barva tohoto
bodu je pak definována hodnotou textury 
. Při programové realizaci většinou postupujeme obráceně: pro
daný bod plochy hledáme na textuře jeho barvu, tj. používáme funkci 
, která je inverzní k původnímu mapování 
. V každém případě jsme dosud dle parametrizace plochy
procházeli všechny její body (v programové realizaci segmenty), každému jsme
přiřadili barvu a každý pak promítli na výstupní zařízení. Tento postup
nanášení textury múžeme označit jako segmentové texturování. Při něm musíme projít
všechny segmenty plochy, mamapovat je a sestrojit, i když mnohé z nich pak
budou překresleny. Nyní budeme postupovat obráceně: budeme procházíme všechny
pixely na výstupním zařízení a každým z nich vyšleme zpětný promítací
paprsek. Protne-li zobrazovanou plochu, obarvíme pixel barvou, která přísluší
nejbližšímu průsečíku, jinak použijeme barvu pozadí. Hlavní výhodou tohoto
postupu je skutečnost, že každý sestrojovaný pixel bude sestrojen „definitivně“
a nebude již překreslován. „Zbytečné kroky“ tak odpadají a konstrukce je
podstatně rychlejší. Docílíme toho následujícím způsobem:
a)
Každému pixelu 
výstupního zařízení
přiřadíme bod 
použité průmětny.
b) Tímto bodem vyšleme zpětný promítací paprsek směrem k zobrazované ploše.
c)
Hledáme jeho průsečíky se zobrazovanou plochou. Jestliže
průsečík neexistuje, testovaný pixel není průmětem žádného bodu a nebude
sestrojen. Jestliže průsečík existuje, pak ho inverzně mapujeme funkcí na texturu a obarvíme
příslušnou barvou (a event. vystínujeme v závislosti na úhlu normály a směru
dopadajícího světla tak, jak bylo rovněž popsáno). Pokud těchto průsečíků
existuje více, mapujeme pouze bod, který je nejblíže pozorovateli.
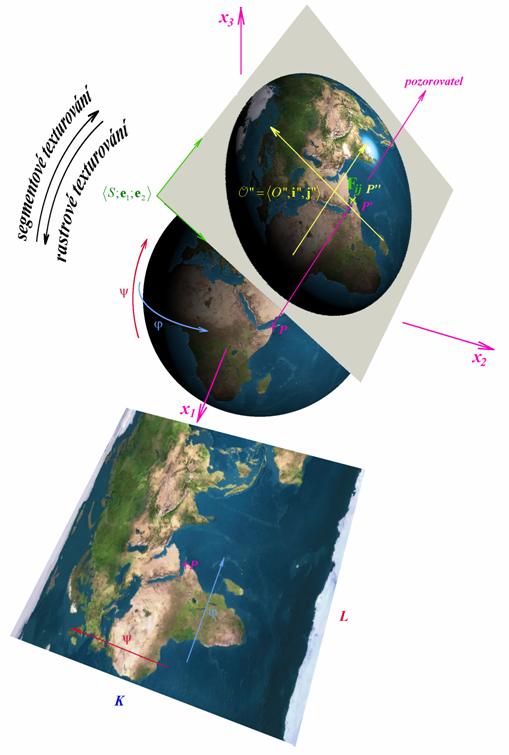
ad a) Především musíme danému
pixelu (tedy bodu ve světové
souřadné soustavě 
) přiřadit uživatelské souřadnice. Jak jsme se zmínili již v
kpt. 7.3., přepočet souřadnic světových na uživatelské provádějí funkce InvXCoor, InvYCoor
- funkce inverzní k XCoor, YCoor. Tím obdržíme průmět 
v uživatelské soustavě
s osami 
. Když jsme se začali zabývat prostorovou grafikou,
konstatovali jsme, že je-li v prostoru definována souřadná soustava 
s osami 
a v průmětně 
uživatelská souřadná
soustava je zobrazení prostoru
na rovinu dáno rovnicemi
kde 
jsou souřadnice
libovolného bodu (tedy například i bod průmětny ) v soustavě 
a 
jsou souřadnice jeho
průmětu 
v soustavě 
.
Nyní ovšem známe průmět 
v uživatelské soustavě
a potřebujeme určit
souřadnice 
odpovídajícího bodu 
v soustavě . Použijeme-li stejnou průmětnu 
jako v kpt.Mp6.1., tj.
průmětnu o rovnici 
, kde 
je vektor definující
směr pohledu do soustavy, dostáváme pro neznámé souřadnice bodu soustavu lineárních
rovnic
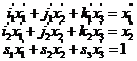
Vzhledem k tomu, že celý postup budeme programovat, je výhodné řešit tuto soustavu Crammerovým pravidlem. Je tedy třeba spočítat determinanty
;
;
;
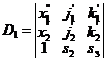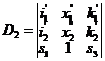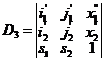; (1)
a potom je 
; 
; 
.
ad b) Takto získaným bodem 
vyšleme zpětný
promítací paprsek 
směrem ke zpracovávané
ploše. Použijeme-li kolmou axonometrii, jsou všechny tyto paprsky kolmé na
průmětnu. Jejich směrovým vektorem je tudíž vektor a parametrické rovnice
jsou
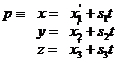(2)
ad c) Dostáváme se k hlavní
potíži tohoto postupu. Ta spočívá v tom, že hledání průsečíku promítacího
paprsku s plochou vede na řešení nelineárních rovnic, které jsou obecně
řešitelné jen numericky, což je nejen značně komplikované, ale především
pomalé. U některých speciálních ploch je však řešení relativně snadné
(například u kvadrik řešíme jen kvadratickou rovnici). Pro kulovou plochu o
rovnici 
kupříkladu dostáváme
po dosazení výše uvedených parametrických rovnic pro hledaný parametr 
kvadratickou rovnici
.
jednoduché úpravě a vzhledem k
tomu, že 
:
Pro hodnotu parametru tak dostáváme
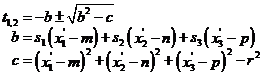(3)
přičemž u odmocniny v tomto
případě uvažujeme pouze znaménko plus. Tím jsme získali hodnotu parametru , pro kterou soustava (2) určuje souřadnice průsečíku
promítacího paprsku s mapovanou kulovou plochou. Pro inverzní mapování
potřebujeme zjistit odpovídající hodnoty parametrů z parametrického vyjádření
kulové plochy. Máme tedy
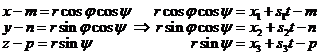(4)
a to pro
; 
; 
(5)
Z poslední rovnice výše uvedené
soustavy (4) tak dostáváme pro 
:
(6)
Vydělíme-li druhou rovnici soustavy
(4) rovnicí první, dostáváme pro 
:
(7)
K řešení rovnic (6), (7)
potřebujeme invertovat funkce sinus a tangens. To lze, jak známo, provést pouze
na intervalech, na kterých jsou tyto funkce prosté. Rovnici (6) můžeme proto
řešit pro 
. To je v souladu s podmínkou (5), máme tedy
(8)
Funkce tangens je však prostá na
intervalech délky p,
přičemž funkce arctg implementovaná v programovacích jazycích vrací hodnoty 
, tj pro 
. Abychom splnili podmínku (5), je třeba rovnici (7) řešit i
na intervalu 
, tj pro 
. Pomocí rovnice (6) máme pro :
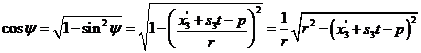
a dosazením do první rovnice
soustavy (4):
tj.
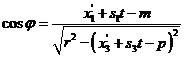
Jmenovatel tohoto výrazu nemůže být záporný, o jeho znaménku tedy rozhoduje znaménko čitatele. To spolu s výše uvedeným znamená, že řešení rovnice (7) je tvaru
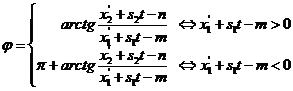(9)
1.
Příklad - Zeměkoule rotující v reálném čase. Úlohu zpracujeme pomocí
rastrového texturování kulové plochy v rovnoběžném promítání, přičemž volíme 
, 
. Nejdříve nadeklarujeme potřebné proměnné. Všechny potřebné
hodnoty (stíny, normály i mapování) bychom samozřejmě mohli počítat bod po bodu
během konstrukce. To by však běh programu značně zdržovalo. Proto je dobré
všechny hodnoty napočítat pokud možno před vlastní konstrukcí a uložit je do
příslušných polí:
type TInvertMap = record x,y :Integer;end;
var Det,Dx1,Dx2,Dx3:Double; {determinanty dle(1)}
OceanShade,
ContShade:Array
[0..600,0..600] of single;
{paměť
pro hodnoty vlastního stínu - zvlášť pro moře a pevninu}
Normala: Array [0..600,0..600] of
TVector;
{paměť
pro normály v jednotlivých bodech kulové plochy}
InvertMap:Array
[0..600,0..600] of TInvertMap;
{paměť pro hodnoty inverzního
mapování}
Stop: Boolean; {zarážka pro ukončení programu}
Dále sestavíme proceduru, která
počítá hodnotu parametru a tím zároveň normálu
kulové plochy ve vypočteném průsečíku - její souřadnice jsou dány pravými
stranami rovnic (3). Tato normála bude potřeba pro výpočet zastínění daného
bodu:
Procedure NormCalcul(i,j:Integer);
var Xc
:T2DPoint;
XPoint :T3DPoint;
Pom,Dx1,Dx2,Dx3,Diskr:Double;
begin
With
Draw3D do
begin {řádky označené r<číslo řádku> budou
použity i v kpt. při sledování paprsku}
Xc[1]:=InvXCoor(i);Xc[2]:=InvYCoor(j);
{SP - uživatelské souřadnice pixelu r1}
{nastavení determinantů podle (1), determinant D (Det) je
nastaven pro všechny body stejně}
Dx1:=k2-MajorRay[2]*k2*Xc[1]-MajorRay[3]*Xc[2];
{SP - nastav determinant D1 r2}
Dx2:=Xc[1]*k2*MajorRay[1]-MajorRay[3]*i2*Xc[1];
{SP - nastav determinant D2 r3}
Dx3:=Xc[2]*MajorRay[1]+Xc[1]*i2*MajorRay[2]-i2;
{SP - nastav determinant D3 r4}
XPoint[1]:=Dx1/Det; {r5}
XPoint[2]:=Dx2/Det; {r6}
XPoint[3]:=Dx3/Det; {souřadnice v prostorové souřadné
soustavě r7}
Pom:=XPoint[1]*MajorRay[1]+XPoint[2]*MajorRay[2]+XPoint[3]*MajorRay[3]; {r8}
Diskr:=Pom*Pom-XPoint[1]*XPoint[1]-XPoint[2]*XPoint[2]-XPoint[3]*XPoint[3]+1; {r9}
if
Diskr>0 then begin {průsečík nalezen r10}
t:=-Pom+sqrt(Diskr); {r11}
Normala[i,j,1]:=XPoint[1]+t*MajorRay[1]; {r12}
Normala[i,j,2]:=XPoint[2]+t*MajorRay[2]; {r13}
Normala[i,j,3]:=XPoint[3]+t*MajorRay[3]; {r14}
end
else begin {průsečík nenalezen r15}
Normala[i,j,1]:=0; Normala[i,j,2]:=0;Normala[i,j,3]:=0; {r16}
end;
end;
end;
Následuje výpočet zastínění:
Procedure Shading(i,j:Integer);
var Cosinus:Double;
begin
With Draw3D do
begin {jestliže byla pro daný bod předchozí procedurou nastavena nenulová normála,}
if Norm(Normala[i,j])>0
{nacházíme se uvnitř průmětu Zeměkoule a stínujeme}
then begin
Cosinus:=abs(CosAngle(Normala[i,j],DirectOfLight));
{moře se leskne víc, než pevnina, proto jsou použity různé funkce}
ContShade[i,j]:=1.15*exp(1.5*ln(Cosinus));
OceanShade[i,j]:=
arctan(sqrt(1-Cosinus*Cosinus)/Cosinus);
OceanShade[i,j]:=(9*exp(-150*OceanShade[i,j]
*OceanShade[i,j])+1)*exp(0.5*ln(Cosinus));
end
else begin {mimo průmět}
OceanShade[i,j]:=1000;ContShade[i,j]:=1000;
end;
end;
end;
Také mapování lze napočítat
předem. V poli InvertMap budou pro každý fyzický pixel 
průmětu kulové plochy
uloženy souřadnice InvertMap[i,j].x resp. InvertMap[i,j].y fyzického pixelu
textury,jehož barvou má být obarven:
Procedure InvertTexturing(i,j:Integer);
var fi,psi:Double;
begin
fi:=arctan(Normala[i,j,3]/sqrt(1-
Normala[i,j,3]*Normala[i,j,3]));
psi:=arctan(Normala[i,j,2]/Normala[i,j,1]);
{hodnoty parametrů
dle (8), (9)}
if Normala[i,j,1]<0 then fi:=fi+pi;
InvertMap[i,j].x:=
Trunc(fi*FormOfTexture.ImageHelp.Width/2/pi);
InvertMap[i,j].y:=
Trunc((psi+pi/2)*FormOfTexture.ImageHelp.Height/pi);
end;
Tělo hlavní kreslící procedury začíná obvyklým nastavením základních parametrů, které zde vynecháme. Dále následuje:
Det:=i1*j2*MajorRay[3]+j1*k2*MajorRay[1]+k1*i2*MajorRay[2]-MajorRay[1]*j2*k1-MajorRay[2]*k2*i1-MajorRay[3]*i2*j1;
{nastavení
determinantu D dle (1)}
With Draw3D do
begin
for i:=0 to
Image.Width-1 do
for j:=0 to Image.Height-1 do NormCalcul(i,j); {normály}
for i:=0 to
Image.Width-1 do
for j:=0 to Image.Height-1 do Shading(i,j); {stínování}
for i:=0 to
Image.Width-1 do
for j:=0 to Image.Height-1 do {inverzní mapování}
if
ContShade[i,j]<1000
then
begin {jsme-li uvnitř průmětu}
InvertMapping(i,j); {výpočet hodnot inverzního mapování}
if
InvertMap[i,j].x>FormOfTexture.ImageHelp.Width
then InvertMap[i,j].x:=InvertMap[i,j].x- {přetečení}
FormOfTexture.ImageHelp.Width;
if InvertMap[i,j].x<0
then {podtečení}
InvertMap[i,j].x:=FormOfTexture.ImageHelp.Width
+InvertMap[i,j].x;
end
else begin {mimo průmět}
InvertMap[i,j].x:=-5000; InvertMap[i,j].y:=-5000;
end;
Origin:=0; {inicializace
počátku textury}
Repeat {procházení
průmětny}
for j:=0 to Image.Height-1 do
begin
SL:=Image.Picture.Bitmap.Scanline[j];
for i:=0 to Image.Width-1 do
if ContShade[i,j]<1000 then
begin
GetTexturePixel {vyzvednutí RGB
složek z textury}
(InvertMap[i,j].x,InvertMap[i,j].y,Red,Green,Blue);
if (Blue<Red) or (Blue<Green) {nepřevažuje-li modrá}
then begin {stínuj kontinent}
RRed:=ContShade[i,j]*Red;
RGreen:=ContShade[i,j]*Green;
RBlue:=ContShade[i,j]*Blue;
end
else begin {jinak stínuj moře}
RRed:=OceanShade[i,j]*Red;
RGreen:=OceanShade[i,j]*Green;
RBlue:=OceanShade[i,j]*Blue;
end;
if RRed>255 {ošetření přetečení a podtečení barev}
then
begin Red:=255;Green:=255;Blue:=255;end
else
begin
if RBlue>255
then begin
Red:=Trunc(255-255/RBlue*188);
Green:=Trunc(255-255/RBlue*60);
Blue:=255;
end
else begin
if RRed<0 then Red:=0
else Red:=abs(Trunc(RRed));
if RGreen<0 then Green:=0
else if RGreen>255
then Green:=255
else
Green:=abs(Trunc(RGreen));
if RBlue<0 then
Blue:=0
else Blue:=abs(Trunc(RBlue));
end;
end; {if RRed...}
Adr:=3*i;SL[Adr]:=Blue;
SL[succ(Adr)]:=Green;
SL[succ(succ(Adr))]:=Red;
end; {for i:=0 to
Image.Width-1 do}
end; {for j:=0 to Image.Height-1 do}
Draw3D.Image.Repaint;
Application.ProcessMessages;
{překreslení
obrazu}{*}
Origin:=Origin+Step; {posunutí počátku textury}
if
Pocatek>FormOfTexture.ImageHelp.Width then
{ošetření přetečení počátku}
Pocatek:=Pocatek-FormOfTexture.ImageHelp.Width;
for
i:=0 to Image.Width-1 do {posunutí textury}
for
j:=0 to Image.Height-1 do
InvertMap[i,j].x:=InvertMap[i,j].x+Step;
until
stop;
{proměnná se nastavuje stiskem tlačítka,událost je
"odchycena" řádkem *}
Na těchto stránkách jsou k dispozici zdrojový i spustitelný kód tohoto příkladu. Příklad lze spustit přímo ze stránek, před svým spuštěním si však do dočasného aadresáře stahuje potřebná data. Pokud by byla v komprimované podobě, bylo by třeba nejdříve stáhnout nějaké dynamicky linkované knihovny (*.dll) a pak teprve příklad spustit. Při tomto spuštění si tedy kód stahuje data ve formátu *.bmp, k jejichž čtení nepotřebuje žádné další knihovny. To je však zaplaceno značnou velikostí příslušných obrázků (celkem cca 15 MB) toto spuštění lze doporučit jen při velmi rychlém připojení
– spustíte zde.
V ostatních případech doporučuji stáhnout a rozbalit
Ten je menší – obsahuje data
v komprimovaném formátu *.png, potřebné knihovny *.dll a dále zdrojové
kódy i kód spustitelný. Po rozbalení tedy můžete soubor spustit ze svého
lokálního disku, popř. pracovat i se zdrojovým kódem
2.
Příklad - Rastrové texturování roviny ve středovém promítání. Ve
středovém promítání je směrový vektor promítacího paprsku určen středem
promítání 
a promítaným
bodem 
, jeho souřadnice jsou tedy 
a parametrické
rovnice promítacího paprsku jsou
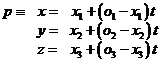(10)
srovnej s rovnicemi (2)
Ve středovém promítání zobrazme
obdélník v rovině kolmé na osu 
. Tento obdélník je určen rovnicemi:
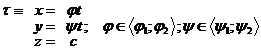
Pro průsečík tohoto obdélníku s promítacím
paprskem dostáváme:
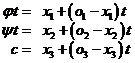
Z poslední rovnice je 
a po dosazení
do zbývajících rovnic máme:
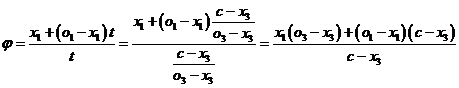
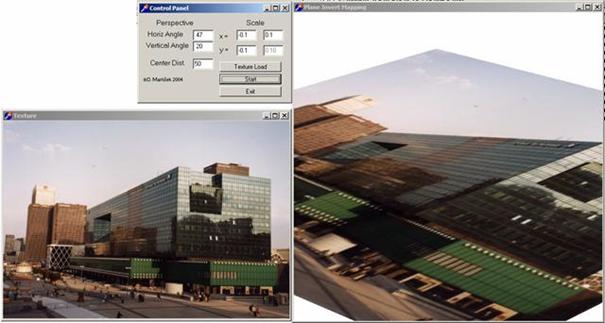
Rastrové texturování roviny tímto
způsobem je velmi rychlé, polohu texturované roviny lze měnit „taháním“ myší.
Rastrové texturování roviny: zde najdete kompletní
zdrojový kód
a zde spustitelný
kód
Odraz světla
Základními zákony geometrické
optiky, které popisují chování světla na rozhraní dvou optických prostředí,
jsou zákon odrazu a zákon lomu. Zákon odrazu ve stručnosti říká, že odražený
paprsek setrvává v rovině dopadu a úhel odrazu se rovná úhlu dopadu. Při
softwarovém zpracování odrazu světla je třeba především zhjistit směr
odtařeného paprsku. Odraz světla na rozhraní dvou optických prostředí je
schématicky znázorněn na připojeném obrázku. Podle zákona odrazu se rovnají
úhly vektorů 
a 
. Tento úhel označme 
. Dále platí, že odražený paprsek zachovává rovinu dopadu,
tj. rovinu určenou vektory 
a bodem dopadu. Označme
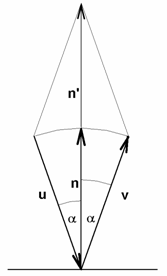
(1).
Vektor 
musí být normálou
v bodě dopadu. Předpokládejme dále, že 
. Pak 
a vzhledem
k tomu, že 
, je
(2).
Protože 
, dostáváme z (2) 
, což dosazeno do (1) dává
(3).
Protože však 
, je 
, podosazení do (3)
tedy 
(4).
Tento vztah dává jednoduchý
návod, jak ze znalosti směru dopadajícího světla a normály v místě dopadu
zjistit směr odraženého paprsku. Odraz světla nebudeme programovat samostatně,
výše uvedeného výsledku využijeme v následujících kapitolách.
Průhledná a průsvitná tělesa
Abychom objasnili průchod světla
průhlednými objekty, je třeba připomenout některé skutečnosti známé z
geometrické optiky. Optické prostředí můžeme považovat za projektivní prostor,
v jehož každém bodě jsou definovány hodnoty nějakých fyzikálních veličin.
(V optice je nejdůležitější index lomu). Hodnoty těchto veličin určují
optické vlastnosti prostředí. Geometrická optika studuje zákony záření založené
na jeho přímočarém šíření. Tyto zákony jsou použitelné v rozměrech mnohokrát
větších než je vlnová délka použitého světla. Při optickém zobrazování se
snažíme dosáhnout toho, aby zobrazení bylo kolineární a navíc projektivní.
Základními zákony geometrické optiky, které popisují chování světla na rozhraní dvou optických prostředí, jsou zákon odrazu a zákon lomu. Zákon odrazu ve stručnosti říká, že odražený paprsek setrvává v rovině dopadu a úhel odrazu se rovná úhlu dopadu. Podle zákona lomu (opět stručně) zůstává lomený paprsek v rovině dopadu a poměr sinů úhlů dopadu a lomu je roven indexu lomu tohoto optického rozhraní. (oba tyto zákony byly přesně formulovány v kpt. Mp4.2. (viz první a druhý zákon). Při modevání průchodu světelného paprsku tenkou vrstvou dochází vpodstatě jen k nepatrnému posunu tohoto paprsku. V kpt. 8.6. jsme tento posun zanedbali, předpokládali jsme, že ke změně směru nedochází vůbec a celou situaci jsme modelovali pouhým mícháním barev. Chceme-li však modelovat průchod paprsku průhledným tělesem nezanedbatelných rozměrů, je třeba vždy pracovat se zákonem odrazu i se zákonem lomu.
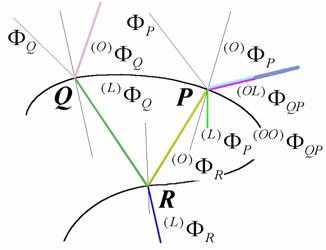
Obraťme nyní pozornost
k tomuto obrázku. Předpokládejme, že do bodu 
dopadá světelný tok 
. Tento paprsek se v bodě 
zčásti odrazí podle
zákona odrazu - odražený paprsek nese světelný tok 
a zčásti lomí
podle zákona lomu - lomený paprsek nese světelný tok 
. Část energie
dopadající do bodu je pohlcena.
V závislosti na vlastnostech objektu v bodě jsou různě pohlcovány
různé vlnové délky a proto jak odražený tok 
, tak prošlý tok nesou (každý jiným
způsobem) informaci o barvě bodu . Zopakujeme-li tuto úvahu pro bod 
, 
, dostáváme světelné toky 
, 
,
, z nichž poslední dva nesou analogicky informaci
o barvě bodu 
. Světelný tok 
však může projít
objektem a dopadnout na další rozhraní v bodě 
, kde se opět zčásti odrazí - 
a zčásti prochází
do dalšího prostředí - 
. Část energie dopadající do bodu je opět pohlcena.
Odražený tok i prošlý tok nesou opět informaci
o barvě bodu . Při vhodné poloze bodů , může odražený tok dopadnout do bodu , kde se opět odráží - 
a láme - 
. Při jisté poloze bodů , mohou paprsky a 
splynout. Takový paprsek
pak nese současně informaci jak o bodu , tak o bodech , 
. Velikosti příspěvků jednotlivých světelných toků pak závisí
jednak na pohlcování určitých složek spektra v jednotlivých bodech, tak na
úbytku vlivem průchodu optickým prostředím.
Při průchodu světla hmotným
prostředím klesá svítivost. Přitom úbytek svítivosti na nekonečně tenké vrstvě
daného prostředí je přímo úměrný aktuální hodnotě této svítivosti, tj. 
. Konstanta této úměrnosti se nazývá index absorbce. Řešením
této rovnice dostáváme:
Lambertův - Beerův zákon: 
, kde 
je svítivost pro 
. Číslo 
nazýváme koeficientem
absorbce.
U většiny látek existuje tzv. selektivní absorbce, která se projevuje tím, že látka pohlcuje světlo o různých vlnových délkách různě. U těchto látek dochází i k selektivní reflexi – různému odrazu v závislosti na vlnové délce.
Při algoritmizaci nelze bohužel většinou postihnout celý popsaný fyzikální proces. Jednak pro celkovou složitost a jednak pro nedostupnost potřebných informací. U každého paprsku by totiž bylo třeba propočítat všechny odrazy a lomy a barvy interferujících paprsků míchat. Navíc by bylo třeba započítat další jevy - absorbci, difuzi, dispersi apod. To ovšem lze udělat pouze pro objekt, který lze popsat analyticky a pro jehož každý bod jsou tyto veličiny známy. Nicméně i při modelování jednoduchých případů je třeba sofwarově modelovat lom světla na rozhraní dvou optických prostředí:
Lom světla je schématicky
znázorněn na připojeném obrázku. Světlo se láme tak, že lomený paprsek
zachovává rovinu dopadu, tj. rovinu určenou vektory a bodem dopadu, a dále
(1)
kde , resp. 
je úhel dopadu, resp.
lomu a 
je relativní index
lomu na rozhraní daných optických prostředí. Vektor 
, který definuje směr lomeného paprsku určíme jako lineární
kombinaci vektorů , tj. platí
(2)
kde 
jsou neznámé
konstanty. Jestliže známe úhel dopadu a index lomu , známe podle (1) i úhel lomu . Předpokládejme, že 
a řešme 
:
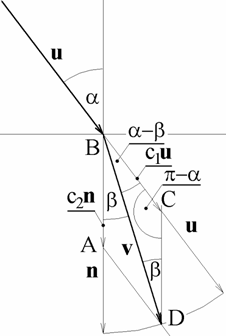
(3)
(4)
Dosazením těchto hodnot do (2)
tedy obdržíme vektor , který definuje směr lomeného paprsku.
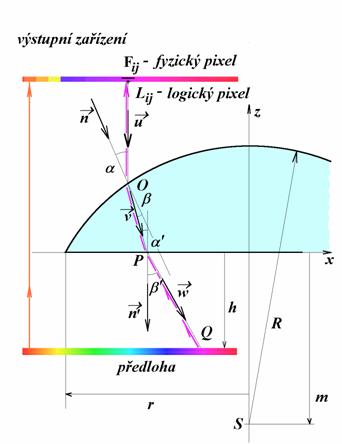
Příklad 1 - Zobrazení silnou spojnou čočkou.
Uvažujme spojnou čočku, která je tvořena kulovou plochou o poloměru a rovinou, která leží
v souřadné rovině 
. Pozorovaná předloha je umístěna ve vzdálenosti 
od této roviny.
Poloměr čočky označme 
. Světelný paprsek vychází z předlohy smětem k výstupnímu
zařízení. Nachází-li se ve vzdálenosti větší než poloměr čočky (měřeno od
optické osy, tedy od souřadné osy ) projde přímo na výstupní zařízení (viz oranžový paprsek).
Nachází-li se ve vzdálenosti menší, musí na cestě k výstupnímu zařízení projít
čočkou (fialový paprsek). Zjistěme, „odkud přišel“ paprsek, který dopadl na
fyzický pixel výstupního zařízení.
Logický pixel, kam paprsek dopadl, má v uživatelské souřadné soustavě
souřadnice 
, v prostoru pak 
, kde hodnota je dána výškou roviny
výstupního zařízení nad rovinou . Sledujme fialový paprsek zpět do místa jeho vzniku. Jeho
první část - úsečka 
má směrový vektor 
a rovnici
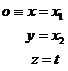
Bod 
, ve kterém se láme na kulové ploše, určíme jako průsečík
kulové plochy a přímky 
:
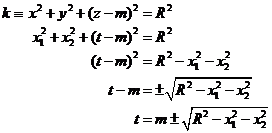
(zde bereme pouze
znaménko plus).
Paprsek se v bodě láme a prochází sklem
po přímce , jejíž směrový vektor je na obrázku označen .Podle zákona lomu zůstává lomený paprsek v rovině dopadu.
Jeho směrový vektor lze tedy napsat
jako lineární kombinaci vektorů 
;
. Koeficienty této lineární kombinace určíme ze vztahů (3), (4). Známe-li směrový
vektor 
paprsku procházejícího
sklem, pak rovnice tohoto paprsku je
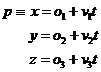
Hledejme průsečík tohoto paprsku s
rovinou 
. Dosazením do poslední parametrické rovnice přímky máme 
, tedy
.
Konečně je třeba najít poslední
část paprsku, která vznikne lomem v bodě rovinného rozhraní
sklo - vzduch. Směr tohoto paprsku je určen vektorem 
. Normála dopadu v bodě nechť má souřadnice 
, pro úhel dopadu pak platí 
. Pro úhel posledního lomu je pak 
. Směrový vektor lomeného paprsku určíme opět jako
lineární kombinaci paprsku dopadajícího a normály dopadu. Postup je analogický, jako u prvního lomu s
jediným rozdílem. K lomu dochází na rozhraní sklo - voda, v příslušné
rovnici je tedy třeba počítat s převrácenou hodnohou indexu lomu skla. Je-li
tedy znám vektor , můžeme napsat rovnici poslední části světelného paprsku
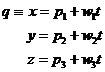
a najít jeho průsečík s rovinou,
ve které leží naše předloha. Pro 
dostáváme z poslední
rovnice 
, takže pro bod vychází 
. Z tohoto bodu je tedy třeba vzít barvu předlohy a přiřadit
ji zpracovávanému pixelu výstupního zařízení.
Chceme-li navíc započítat úbytek intenzity světla vlivem jeho průchodu
prostředím (úbytek přitom většinou předpokládáme pouze ve skle), je třeba
každou barevnou složku vynásobit v souladu s Lambertovým-Beerovým zákonem
výrazem 
, kde je koeficient absorbce
a 
je velikost úsečky 
(délka dráhy paprsku
ve skle).
Zde najdete kompletní zdrojový kód a zde spustitelný kód
Neprochází-li čočkou světlo monochomatické, ale např. světlo bílé, dochází jeho lomem jak známo k rozkladu na spektrální barvy. Tento jev lze modelovat např tak, že každému paprsku nepřiřadíme jeden, ale několik indexů lomu, příslušných několika barvám spektra. Tím odebereme barvu předlohy z několika jejích míst a tyto barvy pak následně sečteme. Tímto způsobem lze modelovat např. barevnou vadu čoček. Výstupy na připojených obrázcích vznikly modelováním bílého světla jako světla skládajícího se z osmi barev, jejichž vlnové délky odpovídají Fraunhofferovým spektrálním čarám.
Zobrazení silnou spojnou čočkou pro bílé světlo:
Zde najdete kompletní zdrojový kód a zde spustitelný kód
Osvětlovací modely
Princip těchto metod objasníme na metodě sledování paprsku, která patří k nejpoužívanějším. Nejdříve je však nutno uvést alespoň několik informací o tzv. osvětlovacích modelech.
Pokud by reálné rovinné optické rozhraní mělo mikroskopicky dokonalý povrch, pak by optický odraz a lom zachovával rovnoběžnost. Jinými slovy - pokud by na takové rozhraní dopadal rovnoběžný svazek paprsků, pak by odražený i lomený svazek byl opět rovnoběžný. Dokonale hladký povrch však žádný reálný přemět nemá. Není-li povrch dokonale hladký, pak normály tohoto povrchu mají různý směr, různé směry mají tedy i odražené a lomené paprsky. Nerovnosti povrchu mají fraktální charakter a vlastnosti odraženého i lomeného svazku lze popsat jen velmi přibližně. Funkci, která se tento charakter snaží popsat, nazýváme odrazovou resp. lomovou funkcí. Aplikaci této funkce v konkrétní situaci pak nazýváme osvětlovacím modelem.
K vyhodnocení odrazu a lomu světla lze přistupovat vpodstatě dvojím způsobem:
a) Fyzikální modely: vycházejí z fyzikálních zákonů šíření světla a odraz od nerovného povrchu se snaží popsat pomocí popisu šíření energie. Tyto metody mohou poskytnout téměř dokonalé fotorealistické výstupy. Jsou však značně složité, časově velmi náročné a pro skutečné výpočty použitelné jen s velkými obtížemi.
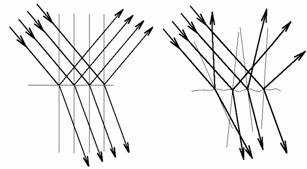
b) Empirické modely: nemají přímý vztah k fyzikální podstatě šíření světla. Chápou složitý fyzikální děj jako černou skříňku a jeho výsledek se snaží více či méně jednoduše kvantifikovat. Nemohou poskytnout tak přesné a vizuálně přesvědčivé výsledky, jako modely fyzikální, jsou však značně jednodušší a aplikace, které jsou na nich založeny, jsou podstatně rychlejší. Jsou proto často používány.
Při fyzikálním popisu je třeba vyjít z definice propustnosti a odrazivosti povrchu. Je známo, že světelný paprsek dopadající na rozhraní dvou optických prostředí se částečně odráží a částečně láme.
Propustnost a odrazivost: Je-li 
svítivost dopadajícího
paprsku, 
resp. 
svítivost lomeného
resp. odraženého paprsku, pak zlomek 
nazýváme
propustnos-tí, zlomek 
odrazivostí.
Propustnost a odrazivost se někdy
udává v procentech. Ze zákona o zachování energie vyplývá 
. Pro odrazivost na dielektrickém rozhraní (např.
vzduch-sklo) platí
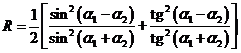
kde 
resp. 
je úhel dopadu resp.
úhel lomu (odvození lze nalézt např. v ). Pro malé úhly, kdy můžeme klást 
, dostáváme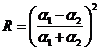 
resp.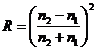 
, neboť zákon lomu přechází pro malé úhly v rovnost 
.
Postupuje-li světlo pod malým
úhlem dopadu ze vzduchu (
) do skla (
), vychází 
, tj. 4% světla se odráží a 96% světla se láme.
Obecně velkou odrazivost mají
kovy. Příčinou je fakt, že světlo dopadající na kov uvede do nucených kmitů
volné elektrony a tyto kmity se skládají s dopadajícím vlněním. Procházející
vlna se tak z velké části zruší a téměř všechno světlo se odrazí. Odrazivost
kovu při kolmém dopadu je dána vzorcem 
, kde je výše uvedený
koeficient absorbce Pro 
dostáváme zřejmě
odrazivost na dielektriku. U kovů se však tento koeficient pohybuje většinou v
rozmezích 2.5 - 4.
Je známo, že index lomu závisí na
vlnové délce světla. Výše uvedená odrazivost tudíž také platí jen pro
monochromatické světlo. V softwarových realizacích je třeba zřejmě znát
odrazivosti (a tedy indexy lomu) pro vlnové délky odpovídající barevným složkám
použitého barevného modelu Red -
; Green - 
; Blue -
(viz kpt Mp4.4. pozn. 15). Ze známých indexů lomu 
, 
, 
pro vlnové
délky 
lze pak určit
index lomu a tím i odrazivost pro libovolnou vlnovou délku 
podle vzorce
Známe-li svítivost 
paprsku dopadajícího na bod plochy a odrazivost plochy v tomto bodě, můžeme vyjádřit odraženou
svítivost 
jako funkci dopadající svítivosti: 
. Je-li uvažovaný
objekt vlastním zářičem, je třeba k celkové zářivosti v daném bodě přičíst
ještě vlastní svítivost 
, tj. 
. Pokud by byla
plocha dokonale opticky hladká, odražené záření by bylo dokonale směrováno.
Takový odraz se nazývá zrcadlový.
Pokud by naopak měly normály povrchu díky jeho mikronerovnostem statisticky
rovnoměrné rozložení, pak by tato plocha odrážela záření rovnoměrně do celého prostoru
bez ohledu na směr dopadajícího světla (byla by kosinovým zářičem dle kpt. Mp.4.1.1.).
Takový odraz se nazývá difuzní. U reálných ploch není žádný odraz dokonale
zrcadlový, ani dokonale difuzní. Za velmi přesný model zrcadlového odrazu však
může sloužit odraz na vyleštěných kovech, za model difuzního odrazu může
sloužit např. odraz na čerstvě napadlém sněhu nebo bílém papíře.
Nejjednoduší empirické osvětlovací modely vycházejí tedy z toho, že celková
svítivost, přicházející z daného bodu k pozorovateli, je dána součtem zrcadlové
a difuzní složky. Většinou se ještě započítává „rovnoměrný příspěvek okolního
světla“ 
. Okolí scény je
fyzikálně řečeno kromě specifikovaných světelných zdrojů osvětleno ještě
sférou, jejíž poloměr roste nade všechny meze a která je kosínovým zářičem.
Řečeno jazykem počítačových grafiků - je to složka, která zabraňuje tomu, aby
plochy odvrácené od světelných zdrojů, byly zobrazeny jako zcela černé. Celková
svítivost je pak dána součtem
Phongův model: je historicky prvním a nejjednoduším empirickým osvětlovacím modelem. V tomto modelu je zrcadlová složka definována jako
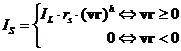
kde je svítivost
dopadajícího paprsku, 
je koeficient
zrcadlového odrazu, který určuje míru zastoupení zrcadlové složky v odraženém
světle. Koeficient 
udává „ostrost
zrcadlového odrazu“. Vektor je normovaný vektor definující
směr pohledu pozorovatele, 
pak směr zrcadlového
odrazu, tj. vektor symetrický s dopadajícím světelným paprskem 
podle normály . Podle vztahu (4) kpt. Mp8.3. tedy platí 
. Je-li 
, nachází se pozorovatel na „odvrácené straně zpacovávané
plochy“ a nemůže odraz vidět. Difuzní složka je dána vztahem:
,
kde 
je koeficient
difuzního odrazu. V případě, že 
je povrch opět
odvrácen od světla a odraz nemůže být vidět.
Celkovou svítivost bodu plochy,
na který dopadá světlo z 
světelných zdrojů pak
počítáme jako 
, kde příspěvek okolního rozptýleného světla (tzv. ambientní
složka) se přičítá jen jednou.
Programová realizace Phongova osvětlovacího modelu je tedy
následující:
function
AmbientComponent : Double; {okolní světlo}
begin
AmbientComponent:= I_A;
end;
function PhongReflex
(N:TVector; {normála povrchu} L:TVector; {směr
dopadu}
V : TVector;{směr pohledu} I_L : Double{intenzita dopadajícího světla} ):Double;
var DiffuseComponent, {difuzní složka}
MirrorComponent:Double {zrcadlová složka}
R :TVector; {směr
zrcadlového odrazu}
NL,VR :Double; {skalární součiny}
begin
NL:=
Draw3D.ScalarProduct(N,L);
if NL > 0 then
DiffuseComponent:= I_L * r_d *NL
else DiffuseComponent:= 0; { povrch je odvrácen od světla}
R[1] := 2*NL*N[1] - L[1];R[2] := 2*NL*N[2] -
L[2];R[3] := 2*NL*N[3] - L[3];
VR :=
Draw3D.ScalarProduct(V,R);
if VR < =0 then
MirrorComponent := 0
else
MirrorComponent := I_L * r_s * exp(ln(VR));
PhongReflex :=
DiffuseComponent + MirrorComponent;
end;
V této implementaci model funguje pro gray scale obraz. Pro barevný obraz je třeba příslušné výpočty provádět pro každou barevnou složku zvlášť a výslednou barvu míchat z takto vypočtených barevných složek.
Sledování paprsku
V reálném světě se světlo šíří ze světelných zdrojů všemi směry. Průchodem optickým prostředím je částečně pohlcováno, na rozhraní dvou prostředí se částečně odráží a částečně láme. Odražený i lomený paprsek pak ovlivňuje další části scény. Informace o scéně pak zprostředkují pouze paprsky, které dopadnou do oka pozorovatele, objektivu fotoaparáfu či kamery nebo jiného snímacího zařízení. Obraz na výstupním zařízení počítače je modelován obarvením bodů zobrazovacího okna. Každý paprsek, který zprostředkuje informaci o zobrazovaných objektech, tak musí projít fyzickým pixelem výstupního zařízení a dopadnout do kamery. Je tedy známa poslední přímka chodu každého paprsku, pomocí níž je třeba zpětně zrekonstruovat jeho předchozí cestu. Podobným způsobem jsme vlastně již postupovali při rastrovém texturování kulové plochy i při modelování spojné čočky. Ve výše uvedených situacích však toto zpětné sledování vypadalo vždycky stejně: V prvním případě paprsek dopadl na kulovou plochu a sledování skončilo. V tomto koncovém bodě bylo třeba zjistit barvu povrchu a úhel normály se směrem světla přicházejícího z jediného světelného zdroje. Ve druhém případě jsme sledovali dva lomy paprsku na rozhraní optických prostředí a po těchto dvou lomech dopadl paprsek na snímanou předlohu. Bylo třeba zjistit barvu předlohy v tomto bodě a (po eventuálním vynásobení koeficientem vyjadřujícím částečné pohlcení) tuto barvu přiřadit příslušnému fyzickému pixelu. V reálném světě však takové zpětné sledování paprsku může dopadnout nejrůznějším způsobem. Některý paprsek projde scénou zcela bez interakce s jakýmkoli objektem a nese tak informaci jen o rozptýleném okolním světle, jiný vznikl ve zdroji světla, dvakrát (třikrát, čtyřikrát...) se odrazil od různých předmětů a teprve pak dopadl do pohledového okna. Jsou -li ve scéně průhledné objekty, původní paprsek se na každém z nich rozdělí na paprsek odražený a lomený a z původního paprsku tak máme paprsky dva (čtyři, osm...).
Základním pojmem metody sledování paprsku je pojem scény. Scénou rozumíme množinu objektů, které se mají zobrazit (reálné objekty), a množinu informací, které lze při tomto zobrazení použít. Přitom tyto informace jsou většinou opět strukturovány jako objekty, které se ovšem nezobrazují (abstraktní objekty).
Scéna tak zahrnuje:
a) kameru - abstraktní objekt (množina informací o pohledové transformaci)
b) světla - abstraktní objekty (informace o poloze a charakteru světelných zdrojů)
c) zobrazované předměty - reálné objekty (informace o objektech, které mají být zobrazeny)
Dále rozlišujeme tři druhy paprsků:
a) paprsek primární - určený pozicí kamery a fyzickým pixelem snímacího zařízení.
b) paprsek sekundární - vzniká odrazem či lomem na povrchu zobrazovaného předmětu.
c) paprsek stínový - spojnice zobrazovaného bodu se světelným zdrojem (slouží ke zjištění, zda je tento bod přímo osvětlen daným světelným zdrojem)
Metoda sledování paprsku spočívá v rekurzivním vyhodnocování všech sekundárních paprsků, které protínají zobrazované předměty ve scéně. Není-li žádný průsečík zjištěn, přiřadí se barva odpovídající barvě pozadí a sledování končí. V praktických situacích by však takové sledování mohlo být velmi dlouhé a dokonce by nemuselo nikdy skončit. Sledování je tedy třeba ukončit nejpozději po předem určeném počtu odrazů či lomů primárního paprsku (toto číslo tak udává maximální hloubku použité rekurze).
Předpokládejme, že se scéna skládá z několika koulí (konstanta NoOfSpheres) a že budeme zpracovávat jen odraz. Celý postup lze popsat např. takto:
Globálně je třeba deklarovat světelný paprsek (Ray), zobrazované koule (Sphere), element scény (Scene_Element) se všemi potřebnými vlastnostmi (fiktivní koncový bod sledovaného paprsku, který s sebou nese všechny potřebné intormace), konstanty nahrazující nulu resp. nekonečno (Like_Zero; Like_Infinity) a hloubku použité rekurze (Level):
Type TRay = record
A,{bod, kterým paprsek
prochází}
s: TVector;{směr paprsku}
end;
TSphere = record
Center
:TPoint;
Radius :Double;
Red,Green,Blue :Byte;
Texture :TBitmap;
Reflex_Component,Diffus_Component,
Red_RefLect,Green_Reflect,
Blue_Reflect :Double;
end;
TScene_Element = record
P:TPoint;
N :TVector;
Red,Green,Blue
:Byte;
Reflex_Component,Diffus_Component,
Red_RefLect,Green_Reflect,
Blue_Reflect:Double;
end;
Const NoOfSpheres=5; Like_Zero = 1e-5;
Like_Infinity=1e5;
Var Ray: TRay;
Sphere: Array
[1..NoOfSpheres] of TSphere;
Scene_Element:TScene_Element;
Level: Byte;
Dále je třeba mít k dispozici funkci, která vrátí paprsek
odražený od zpracovávané plochy známe-li bod a normálu :
Function Reflected_Ray(Ray:TRay;P:T3DPoint;N:TVector):TRay;
Var Scalar:Double; {pomocná proměnná pro skalární součin}
begin
for i:=1 to 3 do Viewing_Direct[1]:=-Ray.s[1];
Scalar:=Draw3D.ScalarProduct(Viewing_Direct,N);
for i:=1 to 3 do Reflected_Ray.s[i]:=
2*Scalar*N[i]-ViewingDirect[i];
for i:=1 to 3 do
Reflected_Ray.A[i]:=P[i]+Paprsek_Odrazu.s[i];
end;
a funkci, která otestuje existenci průsečíku s danou koulí a v případě, že průsečík existuje, vrátí jeho souřadnice s příslušnou normálou:
Function Sphere_Intersect(Sphere:TSphere;
Ray:TRay,
var Point:TPoint,var Norm:TVector):boolean;
(tuto funkci získáme relativně jednoduchou úpravou procedury NormCalcul. Řádky označené zde r8 - r16 všechny potřebné hodnoty počítají. Je třeba je jen upravit podle požadavků zde uvedené hlavičky funkce Sphere_Intersect)
Poté je třeba sesttrojit proceduru, která zajistí texturování kulové plochy. Tento problém jsme již rovněž řešili (viz opět kpt Mp8.2. - procedura InvertTexturing). Zde proběhnou stejné výpočty, některé mezivýsledky však již máme k dispozici, také hlavička procedury bude jiná. Změn je nyní poněkud více, proto vypíšeme celou proceduru:
Procedure SphereTexturing( Sphere:TSphere;
{plocha, kterou je třeba texturovat}
Normal:Tvector {normála});
var fi,psi :Double;
i,j,Adr:Integer;
SL :PByteArray
begin
With
Sphere do
begin
fi:=arctan(
psi:=arctan(
if
i:=Trunc(fi*Sphere.Texture.Bitmap.Width/2/pi);
Adr:=3*i; {mapování
textury}
j:=Trunc((psi+pi/2)*Sphere.Texture.Bitmap.Height/pi); {hodnotu textury
nyní přečteme}
SL:=Sphere.Texture.Bitmap.ScanLine[j];
{z bitmapy, která je součástí
deklarace koule}
Red:= SL[succ(succ(Adr))];
Green:=
SL[succ(Adr)];
Blue:= SL[Adr];
end;
end;
Dále potřebujeme funkci, která otestuje existenci průsečíku
zpracovávaného paprsku se scénou a v případě, že průsečík existuje, vrátí
průsečík a normálu příslušné plochy:
Function Scene_Intersect (Ray:TRay;var
P: TPoint;
var N: TVector): boolean;
var NewPoint:TPoint;NewNormal:TVector;
k,i :integer;
begin
for i:=1 to
3 do Point[i]:=Like_Infinity;
Scene_Intersect:= False;
for k := 1 to
NoOfSpheres do
if
Sphere_Intersect(Sphere[k], Ray, NewPoint, NewNormal) then
if
(sqr(Ray.A.[1]-NewPoint[1])
+sqr(Ray.A.[2]-NewPoint[2])
+sqr(Ray.A.[3]-NewPoint[3])) <
(sqr(Ray.A.[1]-Point[1])
+sqr(Ray.A.[2]-Point[2])
+sqr(Ray.A.[3]-Point[3]))
then begin
Point := NewPoint; Normal :=
NewNormal;
Scene_Intersect := True;
With Scene_Element do
begin
P:=Point;N:=Normal;
Reflex_Componet:=Sphere[k].Reflex_Component;
Duffus_Componet:=Sphere[k].Diffus_Component;
Red_Reflect :=Sphere[k].Red_RefLect;
Green_Reflect :=Sphere[k].Green_Reflect;
Blue_Reflect :=Sphere[k].Blue_Reflect
end;
SphereTexturing(Sphere[k],P);
end;
end;
Konečně je pořeba funkci, která bude rekurzivně sledovat hodnotu barevné složky Red, Green nebo Blue (Color_Component) daného paprsku:
function RayTrack (Ray:TRay; Level:integer; Color_Component:byte): byte;
var Point :TPoint; {dopad sledovaného paprsku na kulovou plochu}
Normal:TVector;
{normála kulové
plochy v bodě dopadu}
Shadow_Point:TPoint;Shadow_Normal:TVector;
{stejné
parametry pro stínový paprsek}
Intensity :Double; {Intenzita světla}
Shadow_Ray TRay; {stínový paprsek}
SecColor :Byte; {barva sekundárního paprsku}
begin
if Scene_Intersect(Ray,Point,
then begin
Intensity:=AmbientComponent;
{nastavení
intenzity pozadí - viz předchozí kapitola}
for k:=1 to NoOfLights do {testování přímého osvětlení světelnými zdroji}
begin
for i:=1 to 3 do {nastavení vektoru
stínového paprsku}
Shadow_Ray.s[i]:=Light_Source[k].Position[i]-Point[i];
Value:=Draw3D.Norm(Shadow_Ray.s);
{normování vektoru stínového paprsku}
for i:=1 to
3 do Shadow_Ray.s[i]:=Shadow_Ray.s[i]/Value;
Shadow_Ray.A:=Light[k].Position;
{počáteční bod vektoru stínového paprsku}
ifScene_Intersect(Shadow_Ray,Shadow_Point,Shadow_Normal)
then {stínový paprsek protíná scénu}
if
sqr(Point[1]-Shadow_Point[1])
//průsečík stínového paprsku splývá s bodem dopadu paprsku světelného, tj. bod je přímo
+sqr(Point[2]-Shadow_Point[2]) // osvětlen
+sqr(Point[1]-Shadow_Point[1]))<Like_Zero
then Intensity:=Intensity+ {přičti příspěvek zdroje}
PhongReflex(N,Incident_Light_Dir,Viewing_Direct,
Light[k].Intensity);
end;
case Color_Component of {podle sledované barevné složky}
1:begin {je sledována červená}
Color:=Scene_Element.Red;
Scene_Element.Reflect_Component:=
Scene_Element.Red_Reflect;
end;
2: {analogicky sledování zelené}
3: {analogicky sledování modré}
else Color:=0;
end;
Color:=Round(Color*Intensity);
if Level>0 then
if Scene_Element.Reflect_Component>0 then
begin
SecColor:=Round(RayTrack(Reflected_Ray(Ray,P,N),
Level-1,Color_Component));
if SecColor>0
then Color:=Color-
Round(Scene_Element.Reflect_Component*(Color-SecColor));
end;
end {if
Scene_Intersect}
else Color:=0;
RayTrack:=Color;
end;
Nyní již zbývá jen nastavit všechny potřebné parametry kamery, světel a zobrazovaných těles (procedura setting - zde je vynechána) a pak již můžeme procházet výstupní zařízení pixel po pixelu a sledovat jednotlivé paprsky:
Procedure
TForm1.RayTracing(Sender:TObject);
begin
Setting; {nastavení parametrů kamery, světel a zobrazovaných koulí}
With Draw3D do {nastavení kamery - pohled do scény}
begin
x1:=...;x2:=...;y1:=...;y2:=...;Scale(x1,x2,y1,y2);
{uživatelské
pohledové okno}
AlfaView:=...;BetaView:=...;ObserverDistance:=...;
{pozice kamery}
SetCenterProjection(AlfaView,BetaView,ObserverDistance,ObserverPoint);
Level:=....; {úroveň rekurze}
for i:=0 to Image1.Height-1 do {procházej pohledové okno bod po bodu}
for j:=0 to Image1.Width-1 do
begin
{Určení souřadnic pixelu v prostorové soustavě
odpovídající pozici kamery viz Mp8.2.př.1}
Ray.A:=ObserverPoint; {zdroj primárního
paprsku}
for m:=1 to 3 do
Ray.v[m]:=XPoint[m]-Ray.A[m];
{směr
primárního paprsku}
Red:=SledujPaprsek(Ray,Level,1); {sledování červené
složky}
Green:=SledujPaprsek(Ray,Level,2); {sledování zelené
složky}
Blue:=SledujPaprsek(Ray,Level,3); {sledování modré
složky}
PutPixel(i,j,Red,Green,Blue); {obarvení pixelu}
end;
end;
end;
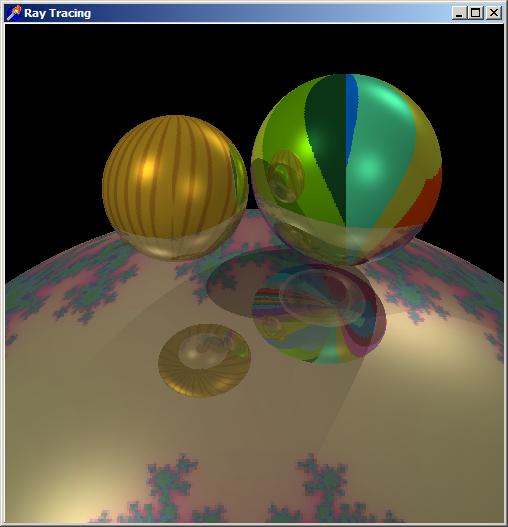
Zde najdete kompletní zdrojový kód a zde spustitelný kód.